[数码] 如果抛开操作系统，直接在裸机上进行除零操作会发生什么情况?

万年历购物网址日历小说 | 三峰软件天天财富小游戏视频推荐小游戏

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

首页日历2023 日历2024 日历2025 日历知识 | 每日头条视频推荐数码知识两性话题情感天地心理咨询旅游天地 | 明星娱乐电视剧职场天地体育娱乐

日历软件煮酒论史历史中国历史世界历史春秋战国三国唐朝宋朝明朝清朝哲学厚黑学心理学 | 文库大全文库分类

电影票房娱乐圈娱乐弱智火研中华城市仙家六爻佛门风水钓鱼双色球戒色航空母舰网球乒乓球足球 nba 象棋体操

知识库 -> 数码 -> 如果抛开操作系统，直接在裸机上进行除零操作会发生什么情况? -> 正文阅读

[数码]如果抛开操作系统，直接在裸机上进行除零操作会发生什么情况?

[收藏本文] 【下载本文】

此外，操作系统和编程语言是如何对这类异常进行检查的呢。

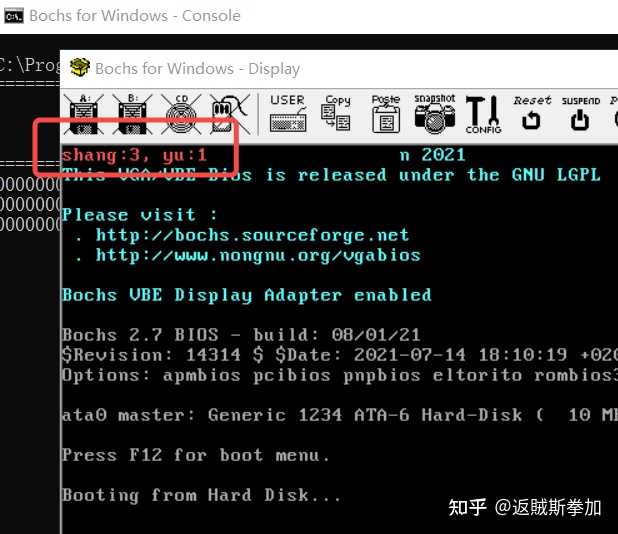
收藏比赞多，大家一起交流一下撒
挺有趣的问题，看了下其他的答案讲的很好，不过裸机运行这块好像理论上面比较多，我来实操一把看看结果（以下代码可以在bochs，qemu，virtualbox这些主流vm中运行，结果相同）
随便写了个一扇区boot，真·裸机运行，先看个正常的，我做个简单的除法 7/3 商2 余1，然后把结果打出来，上代码：

org 07c00h

mov ax, cs
mov ds, ax
mov ds, ax
mov es, ax

call DispStr
jmp $

DispStr:

; ax / bl 也就是 7 / 3 = 商 2 余 1
mov ax, 7
mov bl, 2
div bl

add al, 48 ; 这里是商   
add ah, 48 ; 这里是余数 + 48的原因是要显示了，需要把数字转成对应的ASCII码

mov [BootMessage+6], al
mov [BootMessage+12], ah

mov ax, BootMessage
mov bp, ax
mov cx, 30
mov ax, 01301h
mov bx, 000ch
mov dl, 0
int 10h
ret

BootMessage: db "shang:x, yu:y"

times 510-($-$$) db 0

dw 0xaa55;

上面的代码用
nasm test_div_0.asm -o boot.bin
编译，然后写到一个镜像文件的头512字节里面，也就是硬盘的第一扇区，因为尾部是 0xaa55 魔数，bios会认为这个是个启动扇区，机器加电后会把这512个字节代码加载到内存中来运行，这个时候没有操作系统，可以认为是裸机（不够纯裸的原因是bios里面本身还有rom里面的代码，但这些是写在主板里面的，所以我们可以认为现在就是裸机了）
bochs加载这个镜像如图：

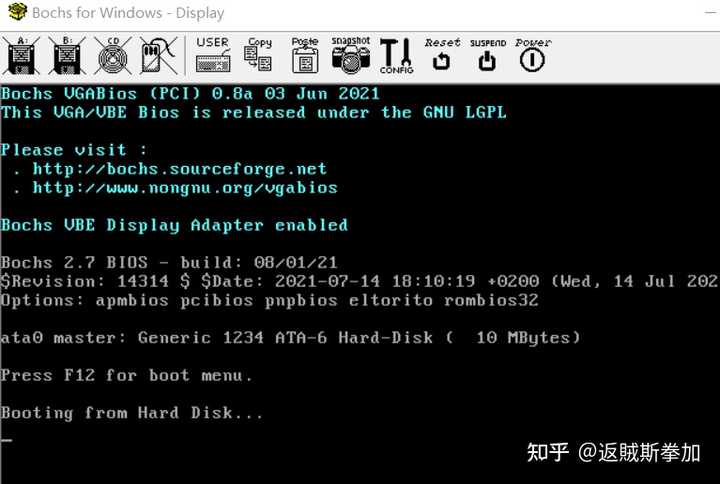
红框我标注了，对着代码，可以认为我们的测试程序成功的进行了7/2的操作
现在来看除0的问题，修改代码

mov ax, 7
;mov bl, 2 注释掉，改为 7/0
mov bl, 0
div bl

运行：

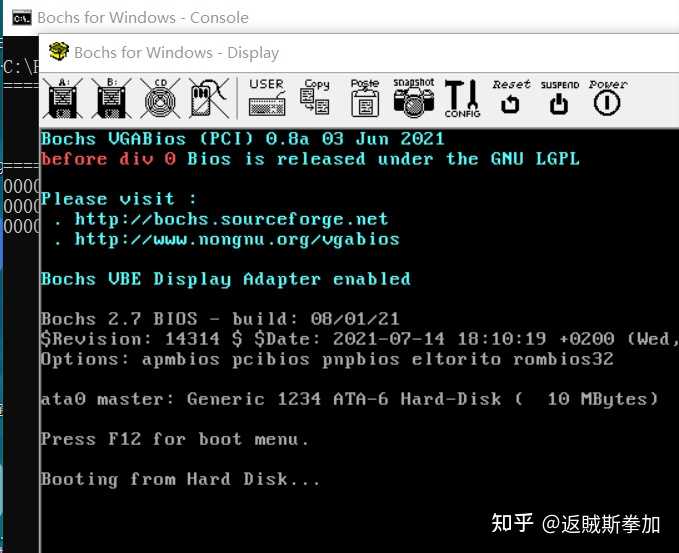
尴尬，没有打印任何东西，我们预想可能会给个除0的error的显示，然而并没有
加点日志看看

org 07c00h

mov ax, cs
mov ds, ax
mov ds, ax
mov es, ax

call DispStr
jmp $

DispStr:



mov ax, Before
mov bp, ax
mov cx, 12
mov ax, 01301h
mov bx, 000ch
mov dx, 0100h
int 10h

; ax / bl 也就是 7 / 0
mov ax, 7
;mov bl, 2
mov bl, 0
div bl

mov ax, After
mov bp, ax
mov cx, 11
mov ax, 01301h
mov bx, 000ch
mov dx, 0200h
int 10h

add al, 48 ; 这里是商   
add ah, 48 ; 这里是余数 + 48的原因是要显示了，需要把数字转成对应的ASCII码

mov [BootMessage+6], al
mov [BootMessage+12], ah

mov ax, BootMessage
mov bp, ax
mov cx, 13
mov ax, 01301h
mov bx, 000ch
mov dx, 0300h
int 10h
ret

BootMessage: db "shang:x, yu:y"

Before: db "before div 0"
After:  db "after div 0"

times 510-($-$$) db 0

dw 0xaa55

运行

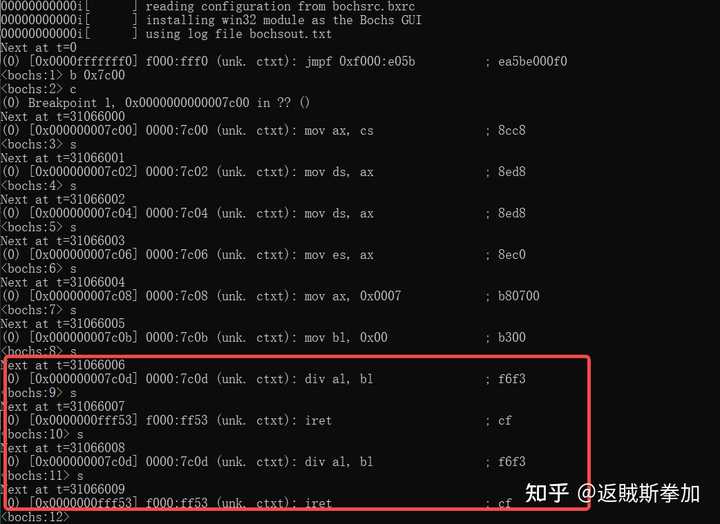
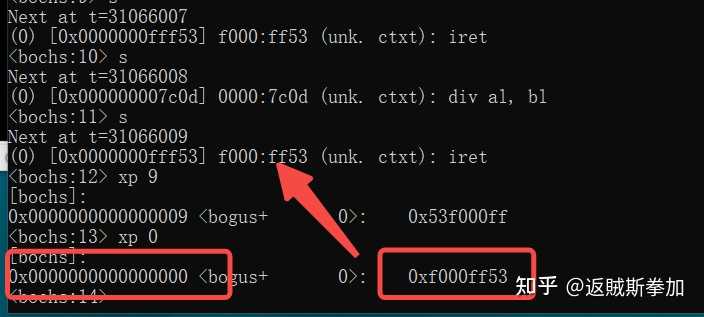
可以看到，只打印了 before div 0，后面的代码都没有运行了
所以，可以回答题主的问题，裸机上面运行除0，会导致CPU除0异常~~~~
不过到底现在是卡死了，还是啥情况，我们不确定，这种情况下，只能断点来看了，写个更简单的除0代码

org 07c00h

mov ax, cs
mov ds, ax
mov ds, ax
mov es, ax


; ax / bl 也就是 7 / 0
mov ax, 7
;mov bl, 2
mov bl, 0
div bl

bochsdebug启动，设置断点，运行到断点，然后单步到div al, bl指令，下一步，会看到跳转到了f000:ff53 位置，执行 iret，又返回了 div al, bl，再一步，又跳转到f000:ff53 位置，执行 iret，反复单步，发现会如此无限循环下去，从单步的结果看这里不是机器重启导致又运行到这里，就是除0中断的反复

现在就是研究一下f000:ff53 这里的iret是什么情况，我们知道bios加电后会把主板上rom中固化的一部分代码加载进内存，并做一些硬件检查和初始化工作，然后才是加载引导扇区（我们的除0代码）
主板rom中bios代码有一些重要功能，读磁盘，显示，等等，这些都是通过bios中断向量表来提供的，中断向量表我们可以理解成一个函数指针数组，数组的下标就是各个中断号，当中断发生的时候，根据中断号查找中断向量表，找到对应的中断函数指针，并且调用，完成后，返回发生中断的指令重新执行
那么我这里猜测 iret 就是除零中断处理函数，f000:ff53就是这个函数的指针（地址），当CPU发生除零时会触发除零中断，然后跳转到f000:ff53执行中断处理程序，不过因为这个中断处理程序啥都没干，直接return了，所以返回后再次执行除零操作，再次引发中断，就这样死循环在这里了
为了验证这一点，我们只要在中断向量表里面看看除0中断的指向的是不是f000:ff53就行了，因为bios的中断向量表是在内存的0号位置开始的，除0中断又是0号中断【这是主板的硬性约定，没有为什么】，所以我们只需要查看内存的0号位置中的内容是不是f000:ff53就行，执行xp 0打印0位置的内存

破案了，0号位置中如果如我们的预期，是base:0xf000 offset:0xff53，刚好就是iret的地址f000:ff53
所以我们可以回答一下答主的问题了
真正意义上的裸机（无bios的情况）除0，我不知道怎么验证传统意义上的裸机（一台可以安装操作系统但还没有安装操作系统情况下的机器）除0，会触发bios除零中断，但是因为这个中断啥也没干，所以会反复触发，计算机就会一直死循环在这里了
注意，以上测试环境是intel x86 cpu，和bochs最新版本的bios代码，如果是另一个主板bios，写出打印除0错误信息也未尝不可
更新一下，操作系统我们除了玩票不会去写的，大都是看看源码，BIOS更是不可能去写了，不过上面已经追踪到BIOS了，不看看里面的还真的不太尽兴，索性看了一下BIOS的源码，确定的上面的猜测
下面的图中的代码都是BIOS，不是操作系统代码，是刷到主板BIOS中的代码

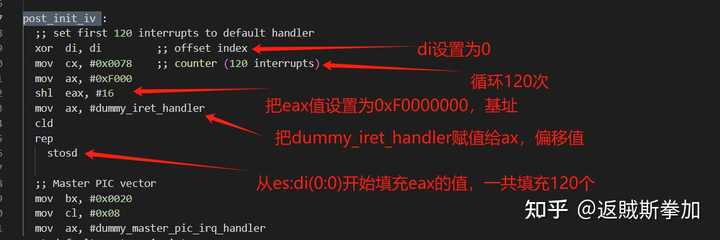
上图可以看出来，这段代码把es寄存器设置为0，并且调用了 post_init_ivt来初始化中断向量表
先普及一个基础知识
rep 指令是指重复执行后面的指令，cx寄存器里面保存了要执行多少次
stos 指令的意思是 mov es:di, ax 也就是将ax寄存器中的值
shl 是左移指令
下面我们看post_init_ivt的实现

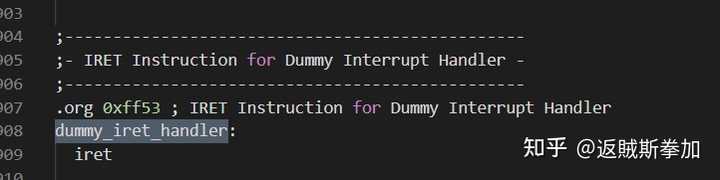
这里就是在初始化BIOS中断向量表，因为es和di都是0，所以是从内存的起始位置开始设置的，中断向量表都是 base:offset的形式，其中base是 0xF0000，那么dummy_iret_handler这个偏移值是多少？

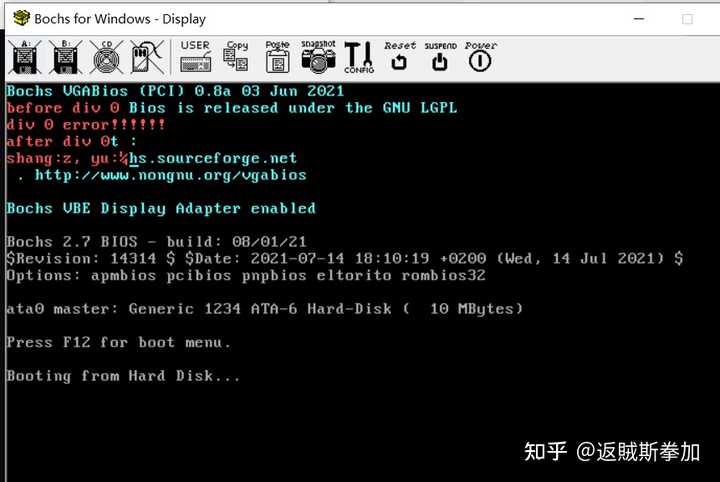
答案是 dummy_iret_handler就是0xff53，所以中断向量表中的base:offset就是 0xf000ff53，和我们上面调试模式下xp 0打印的中断向量表一模一样，所以发生除零异常的时候，CPU的确根据中断向量表跳转到了0xf000ff53，并且执行了iret
看到这里我觉得这个问题算是告一段落了，可以看到BIOS对前120个中断向量都设置为了dummy_iret_handler，也就是说这些中断异常，BIOS并不准备管，BIOS并不会做那么多的事情，它只是提供操作系统编写者必要的功能支持（读磁盘等等），其他的事情都是操作系统加载之后，会重写覆盖中断向量表。
我又来更新啦，因为在评论区中，有小伙伴认为除0中断是严重错误，引起来机器的重启后又走到了除0中断，所以才导致的看上去无限循环在这里，这个推测是错的，除0中断的确是CPU硬布线可以检测到的异常，但是CPU会触发中断，中断必须由相关代码进行处理，BIOS中的dummy_iret_handler就是这样一个中断处理程序
现实中编码遇到除0，后面的逻辑是不能走的，这是严重逻辑错误了，可能程序直接崩了，或者抛出异常，或者像dummy_iret_handler无限循环在哪里，但不管哪种方式都不会再继续执行除零后面的代码了
反正是玩票，我不要你觉得，我要我觉得，我非要除0了不能影响后面的代码执行怎么办？于是我写了个自己的除0中断程序，把BIOS的覆盖掉，遇到除0，打印一个error，然后继续执行代码，纯粹是玩玩，但是也可以看到怎么人为修改iret返回地址，汇编真的很自由 : )

org 07c00h

; 用我自己的除0中断处理函数覆盖BIOS提供的弱鸡处理
; 原理是覆盖内存0起始的第一个中断向量
; 0字节开始的两个字节是IP
; 2字节开始的两个字节是CS
mov ax, Div_0
mov [0], ax
mov ax, 0
mov [2], ax

mov ax, cs
mov ds, ax
mov es, ax

call DispStr
jmp $

; 除0中断处理程序
Div_0:
	; 打印一个 div 0 error!!!!!!
	mov ax, Div0Error
	mov bp, ax
	mov cx, 17
	mov ax, 01301h
	mov bx, 000ch
	mov dx, 0200h
	int 10h
	
	pop ax ; 把中断处理保存的IP丢掉
	mov ax, Div_Out 
	push ax ; 压入除0指令的下一条指令的地址，这样iret后，就会执行下去
	iret

DispStr:



mov ax, Before
mov bp, ax
mov cx, 12
mov ax, 01301h
mov bx, 000ch
mov dx, 0100h
int 10h

; 
mov ax, 7
;mov bl, 2
mov bl, 0
div bl


; 除零中断结束了会直接到这里继续
Div_Out:
add al, 48 ; 这里是商   
add ah, 48 ; 这里是余数 + 48的原因是要显示了，需要把数字转成对应的ASCII码

mov [BootMessage+6], al
mov [BootMessage+12], ah

mov ax, After
mov bp, ax
mov cx, 11
mov ax, 01301h
mov bx, 000ch
mov dx, 0300h
int 10h


mov ax, BootMessage
mov bp, ax
mov cx, 13
mov ax, 01301h
mov bx, 000ch
mov dx, 0400h
int 10h
ret

BootMessage:db "shang:x, yu:y"
Before:     db "before div 0"
After:      db "after div 0"
Div0Error:  db "div 0 error!!!!!!"

times 510-($-$$) db 0

dw 0xaa55

bochs运行

如图
在除0中断发生，正确调用了我自己实现的除0中断处理函数通过改造栈中报错的IP，iret返回的时候直接跳到除0后面的语句继续执行都除0了，再走后面的逻辑本身不对，此处只是娱乐而已，勿当真

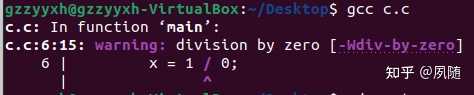
首先，操作系统是不负责检查这些东西的，它只负责把cpu的功能封装起来暴露一些接口给应用软件比如编译器使用，结论，在裸机上做除零操作，肉眼啥也看不到，但是看不见的地方会发生很多有趣的事
先从语言的角度来看，关于除零操作，C 标准明确规定除以零对于整数或浮点操作数都有未定义的行为
C99标准（https://www.open-std.org/jtc1/sc22/WG14/www/docs/n1256.pdf）和C11标准（https://www.open-std.org/jtc1/sc22/WG14/www/docs/n1570.pdf）6.5.5第5段都有提到：

The result of the / operator is the quotient from the division of the first operand by the
second; the result of the % operator is the remainder. In both operations, if the value of
the second operand is zero, the behavior is undefined.

未定义的行为意味着标准没有说明发生的事情，它可能会产生有意义或无意义的结果，可能会崩溃也可能不会，实际上编译器默认会对显式的除0进行告警：

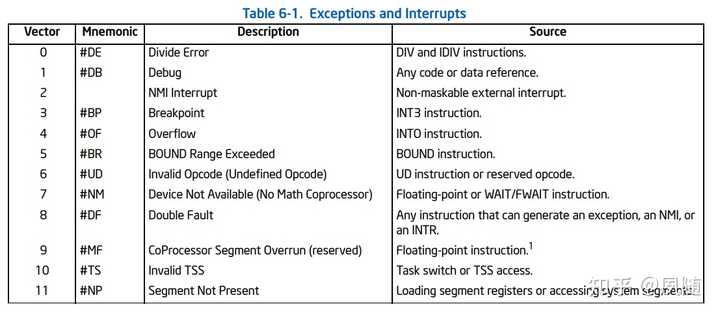
编译通过
gcc在编译过程中抛出一个warning，但这并没有阻止整个编译过程，如果是：

#include <stdio.h>

int main(void)
{
    int x, y = 0;
    x = 1 / y;
    printf("x = %d\n", x);
    return 0;
}

则不会产生warning，可见编译器除了一般性的提示以外，对除零操作是视而不见的
从处理器的角度来看，实际上对“divide by zero”的检查是由cpu里的硬件电路完成的：
根据所有现代C编译器/FPU所使用的IEEE 754标准（http://people.eecs.berkeley.edu/~wkahan/ieee754status/IEEE754.PDF）第10页所描述的，对于浮点数作为操作数的除零运算，将把无穷大作为默认的返回结果：

An example is 3.0/0.0 , for which IEEE 754 specifies an Infinity as the default result. The sign bit of that result
is, as usual for quotients, the exclusive OR of the operands' sign bits. Since 0.0 can have either sign, so can ￥;
in fact, division by zero is the only algebraic operation that reveals the sign of zero. ( IEEE 754 recommends a
non-algebraic function CopySign to reveal a sign without ever signaling an exception, but few compilers offer it,
alas.)

而对于整型数，既不提供inf也不提供NaN，所以处理器只能触发异常（exception），并告诉操作系统终止进程的运行，同时报告错误给用户：

If all goes well, infinite intermediate results will turn quietly into correct finite final results that way. If all does not
go well, Infinity will turn into NaN and signal INVALID. Unlike integer division by zero, for which no integer
infinity nor NaN has been provided, floating-point division by zero poses no danger provided subsequent
INVALID signals, if any, are heeded; in that case disabling the trap for DIVIDE by ZERO is quite safe.

作为验证：当编译并运行以下代码时：

#include <stdio.h>

int main(void)
{
    int x, y = 0;
    x = 1 / y;
    printf("x = %d\n", x);
    return 0;
}

将会给出Floating point exception (core dumped)的错误，注意编译过程是顺利进行的，只有实际在内存中运行时才会出错，这就表明cpu执行到除0时抛出异常，停止当前程序的执行并将控制权返回给操作系统内核（trap），由操作系统处理事件，通常是调用异常处理程序（中断向量表中的某一个条目），打印出异常或诊断信息
而当操作数是浮点数时：

#include <stdio.h>

int main(void)
{
    double x, y = 0;
    x = 1 / y;
    printf("x = %f\n", x);
    return 0;
}

它将打印x = inf，所以对于大多数处理器（RISC-V处理器除外），当遇到“divide by zero”时都会引发异常（FPU也有状态标志，ALU和FPU是并行的），如果是浮点除法，则不会终止进程运行，并且会返回确定的结果inf
以x86架构cpu为例， cpu通过8位的中断类型码通过中断向量表（IDT）找到对应的中断处理程序的入口地址，随即控制权交由操作系统内核进行故障处理，x86体系cpu给每一个中断和异常分配了一个vector number，范围为0-255，一共有256个异常或中断，前32个vector为处理器保留用作异常处理，32-255被指定为用户定义的中断，并且不由处理器保留，中断向量表存在于内存中，如8086PC机的中断向量表指定放在内存地址0处，从0000：0000到0000：03FF的1024个单元里存放中断向量表。Intel? 64 and IA-32 Architectures Software Developer’s Manual Combined Volumes中表6-1列出了部分异常信息：

Exception and Interrupt

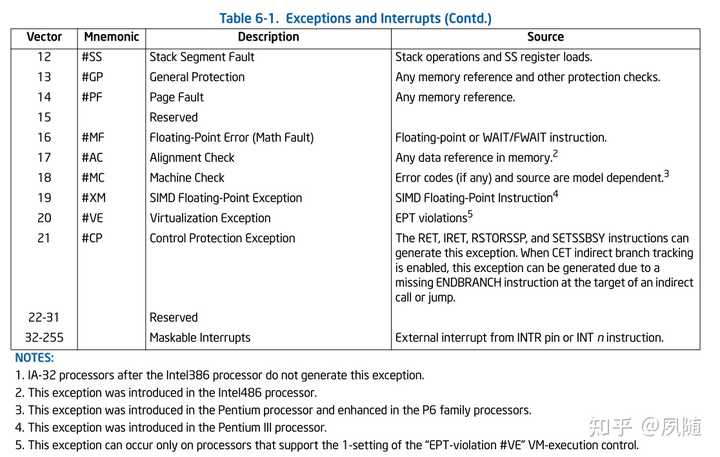
Exception and Interrupt
IA-32和AMD64 ISA将#DE（整数除法异常）指定为中断0，浮点异常触发中断16（x87浮点）或中断19（SIMD浮点），所以整数除零发生时处理器跳转到0号中断处理函数执行，如前所述，告诉操作系统终止当前进程并报告错误信息。
对于浮点数除法（此处仅讨论x87 fpu floating-point exception handling）异常一共有6种情况：

six classes of exception conditions
其中除零的情况在手册8.5.3节有详细说明：

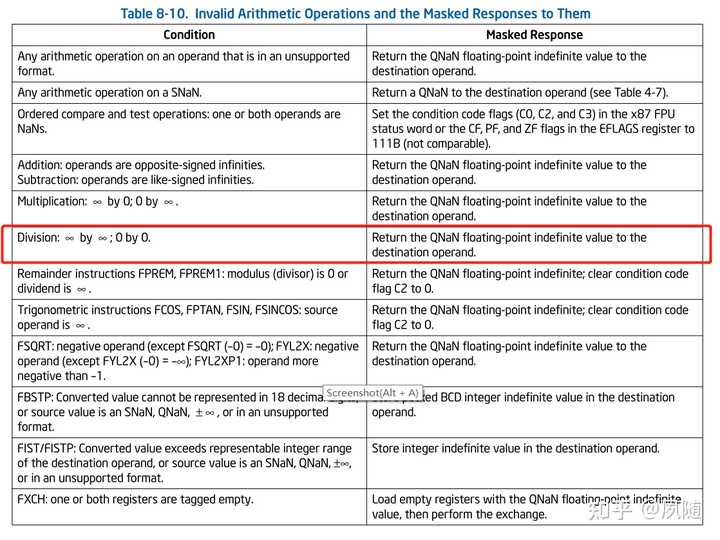
Divide By Zero Exception
可见除0发生时作为结果，x86 cpu返回一个带符号的inf，上面提到的表8-10：

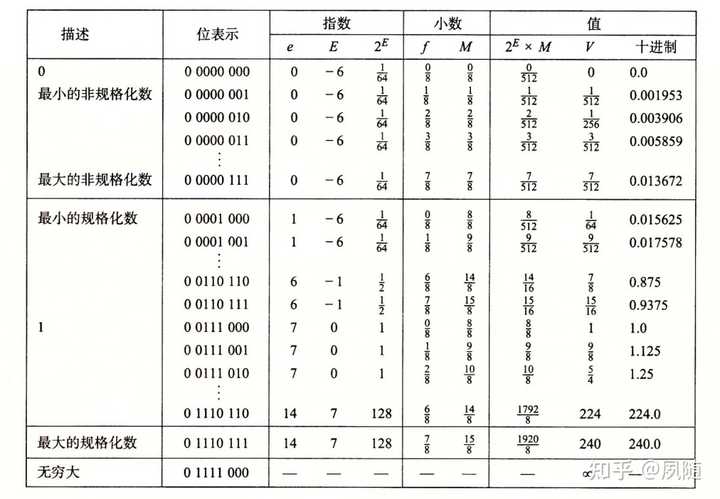
Invalid Arithmetic Operations and the Masked Responses to Them
可见如果是∞ ÷ ∞或0 ÷ 0，x86 cpu的最终结果是返回一个NaN
原文说明如下：
The x87 FPU is able to detect a variety of invalid arithmetic operations that can be coded in a program. These operations are listed in Table 8-10. (This list includes the invalid operations defined in IEEE Standard 754.)
When the x87 FPU detects an invalid arithmetic operand, it sets the IE flag (bit 0) in the x87 FPU status word to 1. If the invalid-operation exception is masked, the x87 FPU then returns an indefinite value or QNaN to the destination operand and/or sets the floating-point condition codes as shown in Table 8-10. If the invalid-operation exception is not masked, a software exception handler is invoked (see Section 8.7, “Handling x87 FPU Exceptions in Software”) and the top-of-stack pointer (TOP) and source operands remain unchanged.
Normally, when one or both of the source operands is a QNaN (and neither is an SNaN or in an unsupported format), an invalid-operand exception is not generated. An exception to this rule is most of the compare instructions (such as the FCOM and FCOMI instructions) and the floating-point to integer conversion instructions (FIST/FISTP and FBSTP). With these instructions, a QNaN source operand will generate an invalid-operand exception.
8.7节就不放在这里了，涉及到中断控制器、中断/异常处理的细节不在这里赘述，至于中断处理函数调用的过程以及具体怎么实现，应该在linux源码里可以找到。
将上面代码中 x =1/ y;替换为x =-1/ y; ,它将打印x = -inf
将上面代码中 x =1/ y;替换为x =0/ y; ,它将打印x = NaN
ISO C99定义了查询和操作浮点状态字的函数，我们可以在方便时使用这些函数检查未捕获的异常，这些常量代表各种 IEEE 754异常。并非所有 FPU 都报告所有不同的异常。当且仅当FPU 支持该异常时，才定义每个常量，它们的定义在fenv.h:

/* FPU status word exception flags */
#define FE_INVALID      0x01  //The inexact exception.
#define FE_DIVBYZERO    0x02  //The divide by zero exception.
#define FE_OVERFLOW     0x04  //The underflow exception.
#define FE_UNDERFLOW    0x08  //The overflow exception.
#define FE_INEXACT      0x10  //The invalid exception.
#define FE_ALL_EXCEPT   (FE_INVALID | FE_DIVBYZERO | FE_OVERFLOW | FE_UNDERFLOW | FE_INEXACT)

整型和浮点型之所以有区别（处理单元、中断处理函数入口不同），是由于浮点数的表示方法与整型不同，浮点变量实际上可以存储表示无穷大的值，而整数无法表示无穷大（整数除法产生的任何位模式都是错误的，因为代表一个特定的有限值），所以只能失败，不能产生NaN或inf作为结果。IEEE浮点标准规定了各种特殊的指数和尾数值，以支持正负无穷和非数（NaN）的概念

IEEE浮点数表示（8位）
NaN（非数字）是以浮点格式编码的符号实体，有两种类型：
Signalling NaN：发出无效操作异常信号Quiet NaN：在几乎所有算术运算中传播而不发出异常信号
NaN由以下操作产生：
∞ - ∞, -∞ + ∞, 0 × ∞, 0 ÷ 0, ∞ ÷ ∞
两种类型的NaN都由格式（单精度或双精度）允许的最大偏差指数和非零尾数表示：
SNaN 的尾数位模式将最高有效位设置为 0，并将其余数字中的至少一个设置为 1QNaN 的尾数位模式的最高有效位设置为 1
除了上面讨论的特殊情况（NaN）外，任何设计无穷大的算数运算都会产生无穷大，无穷大由格式允许的最大偏差指数和零尾数表示
对于单精度值：
正无穷大由位模式7F800000表示负无穷大由位模式FF800000表示SNAN 由7F800001和7FBFFFFFF之间或FF800001和FFBFFFFF之间的任何位模式表示QNAN 由7FC00000和7FFFFFFF之间或FFC00000和FFFFFFFF之间的任何位模式表示
对于双精度值：
正无穷大由位模式7FF0000000000000 表示负无穷大由位模式FFF0000000000000 表示SNaN 由7FF0000000000001和7FF7FFFFFFFFFFFF 之间或 FFF0000000000001FFF7FFFFFFFFFFFF之间的任何位模式表示QNaN 由7FF8000000000000和7FFFFFFFFFFFFFFF 之间或 FFF8000000000000FFFFFFFFFFFFFFFF之间的任何位模式表示
作为验证，编译运行如下代码（GCC12.1/C17）：

#include <stdio.h>
#include <math.h>
#include <stdint.h>
#include <inttypes.h>
#include <string.h>
 
int main(void)
{
    double f = INFINITY;
    uint64_t fn; memcpy(&fn, &f, sizeof f);
    printf("INFINITY:   %f %" PRIx64 "\n", f, fn);
}

它将打印：

INFINITY:   inf 7ff0000000000000

如果我们要在自己的程序中使用无穷大，可以有很多种方法，对于单精度，其中一种是：

#define inf *(float*)&(0x7f800000)

这种方法独立于编译器，适用于任何采用IEEE浮点格式的处理器（x86等），或者更简便的：

#define inf 1.0/0.0

也可以直接使用math.h中的宏INFINITY
在C11 standard (ISO/IEC 9899:2011)中7.12第4段有描述：

The macro
           INFINITY
expands to a constant expression of type float representing positive or unsigned
infinity, if available; else to a positive constant of type float that overflows at translation time.

如果实现支持浮点无穷大，宏 INFINITY 将扩展为浮点类型的常量表达式，其计算结果为正或无符号无穷大。如果实现不支持浮点无穷大，宏 INFINITY 将扩展为一个正值，保证在编译时溢出浮点数，并且使用此宏会生成编译器警告。
而在math.h中有：

#define INFINITY	__builtin_inff()

__builtin_inff()是gcc编译器的内置函数，不需要包含任何头文件即可使用，这个函数返回无穷大，如果打印其返回值：

printf("%f", (double)__builtin_inf());

同样将得到inf
在math.h中还有很多宏可以供我们使用，用来判断一个浮点数是否是无穷大或者有限值：

#define isfinite(x) ((fpclassify(x) & FP_NAN) == 0)
#define isinf(x) (fpclassify(x) == FP_INFINITE)
#define isnormal(x) (fpclassify(x) == FP_NORMAL)

其中：

/*
   Return values for fpclassify.
   These are based on Intel x87 fpu condition codes
   in the high byte of status word and differ from
   the return values for MS IEEE 754 extension _fpclass()
*/
#define FP_NAN		0x0100
#define FP_NORMAL	0x0400
#define FP_INFINITE	(FP_NAN | FP_NORMAL)
#define FP_ZERO		0x4000
#define FP_SUBNORMAL	(FP_NORMAL | FP_ZERO)
/* 0x0200 is signbit mask */

fpclassify()将浮点值分类为zero、subnormal、normal、infinite、NAN或者实现定义的类别，编译运行如下代码（DBL_MIN为float、double、long double的归一化值）：

#include <stdio.h>
#include <math.h>
#include <float.h>
 
const char *show_classification(double x) {
    switch(fpclassify(x)) {
        case FP_INFINITE:  return "Inf";
        case FP_NAN:       return "NaN";
        case FP_NORMAL:    return "normal";
        case FP_SUBNORMAL: return "subnormal";
        case FP_ZERO:      return "zero";
        default:           return "unknown";
    }
}
int main(void)
{
    printf("1.0/0.0 is %s\n", show_classification(1/0.0));
    printf("0.0/0.0 is %s\n", show_classification(0.0/0.0));
    printf("DBL_MIN/2 is %s\n", show_classification(DBL_MIN/2));
    printf("-0.0 is %s\n", show_classification(-0.0));
    printf(" 1.0 is %s\n", show_classification(1.0));
}

将得到：

1.0/0.0 is Inf
0.0/0.0 is NaN
DBL_MIN/2 is subnormal
-0.0 is zero
 1.0 is normal

其具体实现细节也在math.h中：

#define fpclassify(x) \
__mingw_choose_expr (                                         \
  __mingw_types_compatible_p (__typeof__ (x), double),            \
    __fpclassify(x),                                            \
    __mingw_choose_expr (                                     \
      __mingw_types_compatible_p (__typeof__ (x), float),         \
        __fpclassifyf(x),                                       \
    __mingw_choose_expr (                                     \
      __mingw_types_compatible_p (__typeof__ (x), long double),   \
        __fpclassifyl(x),                                       \
    __dfp_expansion(__fpclassify,(__builtin_trap(),0),x))))

以其中的__fpclassifyf（检查单精度）为例，其实现细节也在math.h中：

  __CRT_INLINE int __cdecl __fpclassifyf (float x) {
#if defined(__x86_64__) || defined(_AMD64_) || defined(__arm__) || defined(_ARM_) || defined(__aarch64__) || defined(_ARM64_)
    __mingw_fp_types_t hlp;

    hlp.f = &x;
    hlp.ft->val &= 0x7fffffff;
    if (hlp.ft->val == 0)
      return FP_ZERO;
    if (hlp.ft->val < 0x800000)
      return FP_SUBNORMAL;
    if (hlp.ft->val >= 0x7f800000)
      return (hlp.ft->val > 0x7f800000 ? FP_NAN : FP_INFINITE);
    return FP_NORMAL;
#elif defined(__i386__) || defined(_X86_)
    unsigned short sw;
    __asm__ __volatile__ ("fxam; fstsw %%ax;" : "=a" (sw): "t" (x));
    return sw & (FP_NAN | FP_NORMAL | FP_ZERO );
#endif
  }

其中有一些类型定义，是根据IEEE标准做类型检查的准备：

/* IEEE float/double type shapes.  */

  typedef union __mingw_dbl_type_t {
    double x;
    unsigned long long val;
    __C89_NAMELESS struct {
      unsigned int low, high;
    } lh;
  } __mingw_dbl_type_t;

  typedef union __mingw_flt_type_t {
    float x;
    unsigned int val;
  } __mingw_flt_type_t;

  typedef union __mingw_ldbl_type_t
  {
    long double x;
    __C89_NAMELESS struct {
      unsigned int low, high;
      int sign_exponent : 16;
      int res1 : 16;
      int res0 : 32;
    } lh;
  } __mingw_ldbl_type_t;

  typedef union __mingw_fp_types_t
  {
    long double *ld;
    double *d;
    float *f;
    __mingw_ldbl_type_t *ldt;
    __mingw_dbl_type_t *dt;
    __mingw_flt_type_t *ft;
  } __mingw_fp_types_t;

上面有说到RISC-V处理器不会发生除0异常，这是RISC-V架构为了简化硬件设计，很多RISC架构的处理器（包括其他架构）在运算产生错误时，比如上溢（Overflow）、下溢（Underflow）、非规格化浮点数（Subnormal）和除零（Divide by Zero），都会触发异常跳转（trap）从而进入异常模式，但RISC-V架构的一个特殊之处就是对任何的运算指令错误（包括整数与浮点指令）都不产生异常，而是产生某个特殊的默认值，同时设置某些状态寄存器的状态位，这样可以大幅简化处理器流水线的硬件实现，RISC-V架构推荐软件通过其他方法来找到这些错误。
在RISC-V官方文档Volume I: Unprivileged ISA（https://github.com/riscv/riscv-isa-manual/releases/download/Ratified-IMAFDQC/riscv-spec-20191213.pdf）第7.2节有相关说明：
The semantics for division by zero and division overflow are summarized in Table 7.1. The quotient of division by zero has all bits set, and the remainder of division by zero equals the dividend. Signed division overflow occurs only when the most-negative integer is divided by ?1. The quotient of a signed division with overflow is equal to the dividend, and the remainder is zero. Unsigned division overflow cannot occur.

Semantics for division by zero and division overflow. L is the width of the operation inbits: XLEN for DIV[U] and REM[U], or 32 for DIV[U]W and REM[U]W
We considered raising exceptions on integer divide by zero, with these exceptions causing a trap in most execution environments. However, this would be the only arithmetic trap in the standard ISA (floating-point exceptions set flags and write default values, but do not cause traps) and would require language implementors to interact with the execution environment’s trap handlers for this case. Further, where language standards mandate that a divide-by-zero exception must cause an immediate control flow change, only a single branch instruction needs to be added to each divide operation, and this branch instruction can be inserted after the divide and should normally be very predictably not taken, adding little runtime overhead.
The value of all bits set is returned for both unsigned and signed divide by zero to simplify the divider circuitry. The value of all 1s is both the natural value to return for unsigned divide, representing the largest unsigned number, and also the natural result for simple unsigned divider implementations. Signed division is often implemented using an unsigned division circuit and specifying the same overflow result simplifies the hardware.
下图是Floating-Point Control and Status Register（fcsr寄存器）的编码：

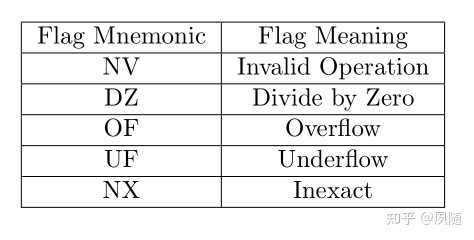
Floating-point control and status register
其包含浮点异常标志位域（fflags），如果浮点运算单元在运算中出现了相应异常，则会将fcsr寄存器中对应的异常标志位设置为高，且已知保持累计，软件可以通过写0的方式清楚某个异常标志位，不同的异常标志位表示的异常类型如下图，官方文档（Volume I: Unprivileged ISA）11.2节给出了详细说明：
The accrued exception flags indicate the exception conditions that have arisen on any floating-point arithmetic instruction since the field was last reset by software, as shown in Table 11.2. The base RISC-V ISA does not support generating a trap on the setting of a floating-point exception flag.

Accrued exception flag encoding.
As allowed by the standard, we do not support traps on floating-point exceptions in the base ISA, but instead require explicit checks of the flags in software. We considered adding branches controlled directly by the contents of the floating-point accrued exception flags, but ultimately chose to omit these instructions to keep the ISA simple.
在11.3节对NaN的情况也有说明：
Except when otherwise stated, if the result of a floating-point operation is NaN, it is the canonical NaN. The canonical NaN has a positive sign and all significand bits clear except the MSB, a.k.a. the quiet bit. For single-precision floating-point, this corresponds to the pattern 0x7fc00000.

AArch64下整数除0的结果为0
RISCV64下整数除0的结果为-1
该结果不受操作系统的影响, 无法通过MSR等方式改变.
X86的整数除0和整数溢出产生陷阱是X86特有的行为(据称IBM大型机用的S390x也是这种行为, 但这种机器比较罕见)
由于在C中整数除0为UB, 因此除非编译器可以静态的确定被除数为0(此时返回值为污染值), 编译器不会做出任何检查. 例如如下代码

#include <stdio.h>
int main() {
  int a, b;
  scanf("%d %d", &a, &b);
  printf("%d\n", a / b);
  return 0;
}

ARM64
在ARM64 macOS上运行

./test
2 0
0

2/0输出结果为0.
Microsoft VC++编译器在AArch64架构下会模拟X86的行为, 总是插入检查代码, 在除0时生成WIN32异常.
RISCV
在RISCV64 Linux上运行

/tmp/test
10 0
-1

10/0结果为-1
RISCV的除法指令为M指令扩展中的div指令, 除此之外还有divu(无符号除)和rem(余数), remu(无符号余数). 其结果定义为如下表格
ConditionDividendDivisorDIVU[W]REMU[W]DIV[W]REM[W]Division by zerox02^L???1x??1xOverflow (signed only)?2^(L?1)??1––?2^(L?1)0
由于RISCV没有历史包袱, 因此32位和64位的行为是一致的.
ARM32
因为ARM32下除法指令是可选的, 因此默认编译器在ARM32/Thumb32下调用__aeabi_idiv函数完成整数除法. 当除数为0时, 该函数调用int __aeabi_idiv0(void), 后者默认返回0, 因此除0仍返回0. 但是可以通过替换该函数的方式定义除0的行为.
在为支持整数除法指令SDIV/UDIV的CPU编译时, 编译器不会生成检查代码. ARM定义这两个指令除0仍返回0.
MIPS
MIPS对除0的结果定义为无法预测的值. 由于MIPS在ISA Spec中建议编译器在div指令后插入检查代码, 因此编译器默认会插入该代码, 除非使用命令行参数-mno-check-zero-division关掉该行为.
例如如下代码:

int div(int a, int b) {
  return a / b;
}

生成汇编

div:                                    # @div
	div	$zero, $4, $5
	teq	$5, $zero, 7
	jr	$ra
	mflo	$2

teq即trap if equal. MIPS架构非常奇葩, 除法的结果要用mflo指令从一对不可见的寄存器hi, lo中搬出来.
LoongArch
LoongArch遵守与MIPS类似的定义: When the divisor is 0, the result can be any value, but no exception will be triggered.
GCC默认只为-O0插入检查代码

-mcheck-zero-division
-mno-check-zero-divison

    Trap (do not trap) on integer division by zero. The default is -mcheck-zero-division for -O0 or -Og, and -mno-check-zero-division for other optimization levels.

LLVM似乎总是不插入检查代码:

div:                                    # @div
	div.d	$a0, $a0, $a1
	addi.w	$a0, $a0, 0
	ret

PowerPC
和MIPS类似, 除0的结果是未定义. 且LLVM似乎总是不插入检查代码. 不过真的还有人在用IBM的处理器吗?
X86
在x86_64 Linux上运行

./test1
5 0
zsh: floating point exception (core dumped)  ./test1

其他回答已经提到了, x86_64下floating point exception(SIGFPE)是Linux将陷阱转换为信号的结果, 裸机代码会直接触发陷阱进入对应的中断处理函数.
Rust编程语言
在Rust中除常量0会导致编译错误, 而虽然LLVM认为整数除0为UB, Rust不允许safe Rust的代码产生UB, 因此会在MIR插入检查. 例如如下代码

fn div(a: i32, b: i32) -> i32 {
    a / b
}

在MIR下是

fn div(_1: i32, _2: i32) -> i32 {
    debug a => _1;
    debug b => _2;
    let mut _0: i32;
    let mut _3: bool;
    let mut _4: bool;
    let mut _5: bool;
    let mut _6: bool;

    bb0: {
        _3 = Eq(_2, const 0_i32);
        assert(!move _3, "attempt to divide `{}` by zero", _1) -> [success: bb1, unwind continue];
    }

    bb1: {
        _4 = Eq(_2, const -1_i32);
        _5 = Eq(_1, const i32::MIN);
        _6 = BitAnd(move _4, move _5);
        assert(!move _6, "attempt to compute `{} / {}`, which would overflow", _1, _2) -> [success: bb2, unwind continue];
    }

    bb2: {
        _0 = Div(_1, _2);
        return;
    }
}

在X86汇编上是

playground::div:
	pushq	%rax
	testl	%esi, %esi
	je	.LBB0_4
	cmpl	$-2147483648, %edi
	jne	.LBB0_5
	cmpl	$-1, %esi
	je	.LBB0_3

.LBB0_5:
	movl	%edi, %eax
	cltd
	idivl	%esi
	popq	%rcx
	retq

.LBB0_4:
	leaq	str.0(%rip), %rdi
	leaq	.L__unnamed_1(%rip), %rdx
	movl	$25, %esi
	callq	*core::panicking::panic@GOTPCREL(%rip)
	ud2

.LBB0_3:
	leaq	str.1(%rip), %rdi
	leaq	.L__unnamed_1(%rip), %rdx
	movl	$31, %esi
	callq	*core::panicking::panic@GOTPCREL(%rip)
	ud2

.L__unnamed_2:
	.ascii	"src/lib.rs"

.L__unnamed_1:
	.quad	.L__unnamed_2
	.asciz	"\n\000\000\000\000\000\000\000\002\000\000\000\005\000\000"

str.0:
	.ascii	"attempt to divide by zero"

str.1:
	.ascii	"attempt to divide with overflow"

可见需要检查3次, 即除数为0, 或被除数为MIN且除数为-1.
不像整数溢出, Rust对除0的检查在Release模式下也无法关闭, 因此Rust在操作系统下和在裸机下除0总是会panic.
Rust提供checked_*系列函数, 在遇到各种溢出和除0时返回None, 这样就不会触发panic, 而是由用户决定如何处理Option结果.
checked_div的源码如下, 其中unchecked_div对应C/C++的语义.

        #[inline]
        pub const fn checked_div(self, rhs: Self) -> Option<Self> {
            if unlikely!(rhs == 0 || ((self == Self::MIN) && (rhs == -1))) {
                None
            } else {
                // SAFETY: div by zero and by INT_MIN have been checked above
                Some(unsafe { intrinsics::unchecked_div(self, rhs) })
            }
        }

WebAssembly
WebAssembly是一种虚拟机指令集, 我调查整数除0的问题就是因为我编写的WebAssembly编译器在测试官方的测试套件时报错.
WebAssembly的spec虽然说整数除0和整数除法溢出的结果是未定义, 但实际上要求产生Trap. 因此WebAssembly是和X86一样唯二整数除0产生陷阱的架构.

大多数现代高级语言（如BASIC、Python、Java等）在遇到除法时会先检查除数，为零则有会相应的对策（报错、抛出异常等）提前拦截，CPU不会真正执行除零。
而C语言则不会检查除数，并假设除数非零，直接编译生成CPU除法指令机器码。
而CPU执行除零时的行为，则与指令集的定义和具体的逻辑电路设计有关。
比如大家熟悉的8051，只有一条除法指令DIV AB，把寄存器A和B相除，执行后A为商，B为余数。如果B为0，则执行后A、B中的值为未定义（意思是可由MCU厂家在设计内核电路时任意处理，一般是保持不变），溢出标志OV置1（如果B不是0则OV总是被清零），然后继续执行下一条指令，没有什么特殊的事件发生。
而ARM则会触发异常（类似中断），跳转到异常向量执行中断程序。
操作系统能否捕获除零异常也是建立在CPU架构设计之上。
在ARM这类CPU上，由硬件中断捕获除零，在异常处理程序中向操作系统内核报告错误。
在8051这类CPU上，没有硬件的协助，只能依靠软件检查。好的库函数会事先检查除数，或者事后检查OV标志。其实大多数情况是不去管它，放任未定义的结果。
最后，避免除零错误是编码者的责任。硬件和OS的异常保护机制不是用来帮你的烂代码擦屁股滴~

解答一下这位的疑问。
C语言（出于追求极致效率的考量）规定，当除数为零时，除法和取余为未定义行为（undefined behavior，简称UB）。这意味着，C编译器大可直接生成CPU除法指令。除数非零时效率最高（因为没有事前事后的检查步骤）；除数为零时把UB的锅甩给CPU指令集。

int a = 3/0;

这句的赋值号右边是编译期常量，编译器会直接算出结果再赋值。但3/0算不出来，所以编译器会给出警告，但依然仍能编译通过。具体生成什么样的机器码不得而知。
如果改成

int a = 3, b = 0;
int c = a/b;

那么，比较优质的编译器（比如GCC）会分析出此时b实际上为0而给出警告，但仍会按语义生成除法指令。次一些的（比如一些适配特殊指令集的闭源C编译器）就不会有任何警告了。
设计一门语言要平衡诸多利益，C语言亦不例外。C的取舍是追求极致的效率，因此高度信任编码者。熟悉C语言的编码者能与编译器琴瑟和谐，相得益彰，输出高效的机器码。
C中规定的UB几乎都是高手不会犯的低级错误，C不愿为了预防它们而损失效率，定为UB也算是一种甩锅行为吧。
最后基于
@墨枫梧桐BA7MQN
的高见，再补充2句：C编译器的warning其实是增值服务，是编译器作者的经验结晶。C编译器对UB给出warning只是出于道义，而不是义务。

和操作系统没有任何关系，只和cpu有关系。

[收藏本文] 【下载本文】

数码最新文章

iOS的墓碑机制这么厉害，为什么Windows、Li

如何看待华为发布会被指造假？

如何看待华为 Pura 70 系列超高速风驰闪拍功

碎纸机是干嘛用的，撕个纸还要用机器，真是

小米真的是为国为民吗？

华为发布 MatePad 11.5 S 平板电脑，该产品

加:2024-01-09 10:32:43 更:2024-01-09 10:37:06

娱乐生活: 电影票房娱乐圈娱乐弱智火研中华城市印度仙家六爻佛门风水古钱币交流专用钓鱼双色球航空母舰网球乒乓球中国女排足球 nba 中超跑步象棋体操戒色上海男科 80后
足球: 曼城利物浦队托特纳姆热刺皇家马德里尤文图斯罗马拉齐奥米兰里昂巴黎圣日尔曼曼联

网站联系: qq:121756557 email:121756557@qq.com 知识库