| |
|
| 知识库 -> 数码 -> 为什么在10进制体系下可以写下“10”,而在二进制体系下写不出“2”? -> 正文阅读 |
|
|
[数码]为什么在10进制体系下可以写下“10”,而在二进制体系下写不出“2”? |
| [收藏本文] 【下载本文】 |
|
今日看一问题说“为什么10进制有10,而二进制没有2?”这个问题我自然是已经略微知晓了的,但我转念一想,如果将这里数字视为一个文字,在平日里所用的10… |
|
十进制下能写出10, 二进制下不能写出2, 问题的原因就在于这个“2”,它并不是二进制里面的东西,而是十进制里面的。 事实上和十进制下能写出10对等的命题是, 二进制下能写出10(注意,这个是二进制下的2,而不是十进制下的十) 而和二进制下写不出2对等的命题是, 十进制下写不出A(十六进制的十) |
|
兄弟, 16进制数每一位上有0123456789abcdef。 10进制数每一位上有0123456789。 8进制数每一位上有01234567。 2进制数每一位上有01。 每一位上述都只占一位。 而你问题中的10进制“10”已经是两位数了。请写一个十进制中一位数的“十”出来。然后咱们再来讨论这个问题,谢谢。 |
|
多稀奇? 你十进制也写不出 A 啊。 |
|
二进制也可以写出二 :=10" role="presentation">:=10:=10 这是故意混淆概念而提出的问题。进制由字母表和表示规则决定。对于进制 B" role="presentation">BB ,设定字母表为有限集合 Σ" role="presentation">Σ\Sigma ,则该进制下的一个数定义为 Σ" role="presentation">Σ\Sigma 中的字母组成的有限字符串的集合,记作 N(B):=⋃n=1∞Σn" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">N(B):=?n=1∞Σn\mathscr{N}(B):=\bigcup_{n=1}^\infty\Sigma^n\\记 X" role="presentation">X\mathcal{X} 是一个数集,则表示规则是某个 N(B)→X" role="presentation">N(B)→X\mathscr{N}(B)\to\mathcal{X} 的映射,为每一个字符串指定了其“值”或者“大小”。这个映射的像 im[N(B)→X]⊂X" role="presentation">im[N(B)→X]?X\text{im}[\mathscr{N}(B)\to\mathcal{X}]\subset\mathcal{X} 称为这个进制的表示范围,记作 R(B)" role="presentation">R(B)\mathscr{R}(B) 。 例子:设 0}">j∈Z>0" role="presentation">j∈Z>0j\in\mathbb{Z}_{>0} ,我们定义所谓的 j−" role="presentation">j?j- 进制 Bj" role="presentation">BjB_j 如下 ∘" role="presentation">°\circ 字母表 Σj={0,⋯,j−1}" role="presentation">Σj={0,?,j?1}\Sigma_j=\{0,\cdots,j-1\} ,共 j" role="presentation">jj 个可用字母; ∘" role="presentation">°\circ 表示规则是映射 N(Bj)→N,  (dn,⋯,d0)↦∑k=0ndkjk" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">N(Bj)→N, (dn,?,d0)?∑k=0ndkjk\mathscr{N}(B_j)\to\mathbb{N},~~(d_n,\cdots,d_0)\mapsto\sum_{k=0}^nd_kj^k\\ ∘" role="presentation">°\circ 很容易证明,这个映射是满射,因此表示范围 R(Bj)=N" role="presentation">R(Bj)=N\mathscr{R}(B_j)=\mathbb{N} 。(这顺便是单射,所以给出了 |⋃n=1∞Σn|=ℵ0" role="presentation">|?n=1∞Σn|=?0\big|\bigcup_{n=1}^\infty\Sigma^n\big|=\aleph_0 的一个证明) 注意到 B2" role="presentation">B2B_2 就是所谓的二进制,而 B10" role="presentation">B10B_{10} 是我们常用的十进制。现在,这个问题应当被重新表述为:为什么 10∈R(B10)" role="presentation">10∈R(B10)10\in\mathscr{R}(B_{10}) ,而 2∉Σ2" role="presentation">2?Σ22\notin\Sigma_2 (为什么 10" role="presentation">1010 属于十进制的表示范围,而 2" role="presentation">22 不属于二进制的字母表)呢?一旦解读这问题如上,再无任何疑虑。 尽管与本问题无关,但是进制带来的另一常见困惑也来源于概念的混淆。定义带小数的十进制: ∘" role="presentation">°\circ 字母表仍取为 Σ10" role="presentation">Σ10\Sigma_{10} ,但数对应的集合修改为 N∗(B10):=N(B10)×{.}×Σ∞" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">N?(B10):=N(B10)×{.}×Σ∞\mathscr{N}^*(B_{10}):=\mathscr{N}(B_{10})\times\{.\}\times\Sigma^\infty\\也即,带小数的十进制中一个数由三部分组成,小数点左侧是一个有限长的十进制串,右侧是一个无限长的序列。 ∘" role="presentation">°\circ 表示规则是映射 N∗(B10)→R,  ((dn,⋯,d0),⋅,{tj}j≥1)↦∑j=0ndj⋅10j+∑j=1∞tj10j" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">N?(B10)→R, ((dn,?,d0),?,{tj}j≥1)?∑j=0ndj?10j+∑j=1∞tj10j\mathscr{N}^*(B_{10})\to\mathbb{R},~~\big((d_n,\cdots,d_0),\cdot,\{t_j\}_{j\ge1}\big)\mapsto\sum_{j=0}^nd_j\cdot10^j+\sum_{j=1}^\infty\frac{t_j}{10^j}\\ ∘" role="presentation">°\circ 这个映射是满射,但并不是单射。这就是说,相同的实数可能有不同的十进制表示方法。 例子(万恶之源):定义 d0:=1,tj:=0  (j≥1)" role="presentation">d0:=1,tj:=0 (j≥1)d_0:=1,t_j:=0~~(j\ge1) ,此时有 (1,⋅,{tj}j≥1)↦1∈R" role="presentation">(1,?,{tj}j≥1)?1∈R\big(1,\cdot,\{t_j\}_{j\ge1}\big)\mapsto1\in\mathbb{R} 。利用 ∑j=1∞110j=109" role="presentation">∑j=1∞110j=109\displaystyle\sum_{j=1}^\infty\frac{1}{10^j}=\frac{10}{9} ,可以发现若定义 d0′:=0,tj′:=9  (j≥1)" role="presentation">d0′:=0,tj′:=9 (j≥1)d_0':=0,t'_j:=9~~(j\ge1) ,仍然有 (0,⋅,{tj′}j≥1)↦1∈R" role="presentation">(0,?,{tj′}j≥1)?1∈R(0,\cdot,\{t_j'\}_{j\ge1})\mapsto1\in\mathbb{R} 。这个结论用通俗的记号写就是 0.9∙=1" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">0.9?=10.\overset{\bullet}{9}=1\\ |
|
题主说的没错,10进制是很特殊的,因为所有进制都是10进制 |
|
大春,你和其他人不一样,千万别把时间浪费在学习上 |
|
在 any 进制体系下都可以写出“10”,而在N进制体系下都写不出N。 所以在十进制体系下可以写出“10”,而在二进制体系下写不出“2”。 |
|
十进制你也没办法用一位数写出 10,你必须进位之后用两位数写出 10。同理,二进制不能用一位数写出 2,只能进位后把 2 写作 10。 |
|
一、结论 不仅二进制所含的数字没有 2,十进制所含的数字也没有 10 1、十进制没有 10 2、二进制没有 2 二、原理 十进制指的是以 10 为底的进制(数字元素为 0 - 9)表示。二进制是以 2 为底的进制(数字元素为 0 和 1)表示。 1、十进制计数拆解 比如,10 这个数字,其实是 1 乘以 10 的 1 次方,再加上 0 乘以 10 的 0 次方。 |
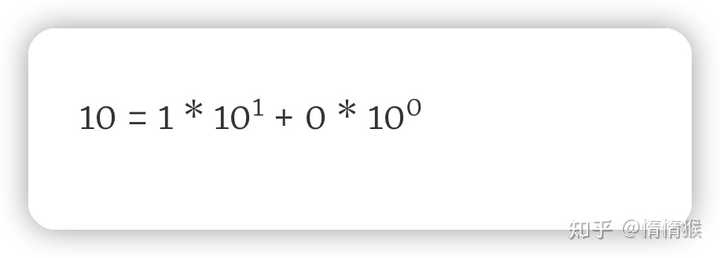
|
|
10 = 1 * 10^1 + 0 * 10^0 再比如,32 这个数字,其实是 3 乘以 10 的一次方,再加上 2 乘以 10 的 0 次方。 |

|
|
32 = 3 * 10^1 + 2 * 10^02、二进制计数拆解 比如,二进制的 10 ,就相当于十进制的 2。 |

|
|
10 = 1 * 2^1 + 0 * 2^0 再比如,二进制 1010 ,就相当于十进制的 10。 |
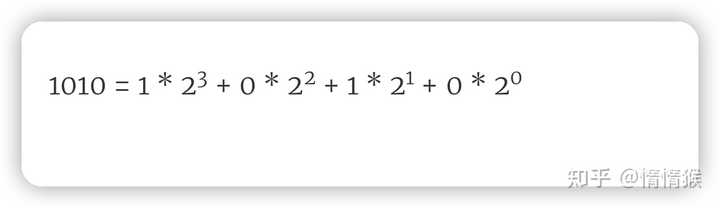
|
|
1010 = 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^03、举一反三 比如,再举一例,二进制 100000 ,就相当于十进制的 32。 |
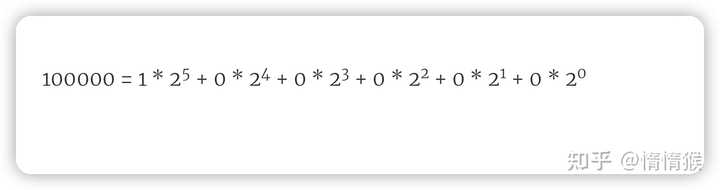
|
|
100000 = 1 * 2^5 + 0 * 2^4 + 0 * 2^3 + 0 * 2^2 + 0 * 2^1 + 0 * 2^0 |
|
这让我想到了之前的一个笑话:这个世界上只有10种人,一种是懂二进制的人,一种是不懂二进制的人,还有一种是以为这是个二进制笑话的人。 不妨来想想,笑话里的“10种人”,到底是指几种呢? 答案可以是任意种,主要看语境是在几进制里。 十进制里10就是10,二进制里10就是2。 N进制下, 10=1∗N1+0∗N0=N" role="presentation">10=1?N1+0?N0=N10=1*N^{1}+0*N^{0}=N 写到这里,我再分享一道和进制有关的算法题。 非常有趣,相信看完后会对这个提问的理解更深一步。 原算法是在 matrix67[1] 那里看到的,非常非常有意思,给人印象深刻。 题目是——猜出多项式的各项系数: 有一个黑匣子,黑匣子里有一个关于 x" role="presentation">xx 的多项式 p(x)" role="presentation">p(x)p(x) 。我们不知道它有多少项,但已知所有的系数都是正整数。每一次,你可以给黑匣子输入一个整数,黑匣子将返回把这个整数代入多项式后的值。那么,最少需要多少次, 我们可以得到这个多项式每项的系数呢? 答案是:两次 首先,输入 1" role="presentation">11 ,于是便得到整个多项式的所有系数之和,把这个系数和记作 S" role="presentation">SS 。 下一步,输入 S+1" role="presentation">S+1S + 1 ,于是黑匣子返回 an∗(S+1)n+an−1∗(S+1)n−1+…+a1∗(S+1)+a0" role="presentation">an?(S+1)n+an?1?(S+1)n?1+…+a1?(S+1)+a0a_{n} * (S + 1)^{n} + a_{n-1} * (S + 1)^{n-1} + … + a_{1} * (S + 1) + a_{0} 把这个值转换成 S+1" role="presentation">S+1 S + 1 进制,依次读出每一位上的数,它们就是多项式的各项系数啦~ |

|
|
|

|
|
|

|
|
参考^http://www.matrix67.com/blog/archives/4064 |
|
我们只需要理解两个概念,就不难理解这个问题。 第一,整数是一种抽象存在。 为了表示这种抽象,我们把数字用汉字来表示,而不用阿拉伯数字。 这是『三个苹果』,客观上就是有『三』个东西在这里。 |

|
|
围棋棋盘上有『三百二十四』个格子,这个『三百二十四』是一个客观存在的数字,只是这里既然用了『百』和『十』,代表就是十进制表示。 |

|
|
当我们说一个客观数字的时候,总是倾向于默认用十进制表示。 第二,任何进制都只是数字的一种表示方式。 客观上同样一个数字,在不同进制下的表示方式可能(注意是可能)不一样,比如『三个苹果』,在十进制下表示是3,在二进制下表示是11,在八进制下还是3。 好,现在回到这个问题——为什么在10进制体系下可以写下“10”,而在二进制体系下写不出“2”? 因为『可以写下10』,这个『10』被我们大脑默认代表数字『十』,暗含了『客观数字十』的含义,换句话说,我们大脑里不自觉把数字的抽象和数字的表示方式混合在一起了。 我们习惯上各种进制都用阿拉伯数字0,1,2...,9表示,十进制以上用上A,B,C...这些符号,但是这些单个符号也就是一个符号,我们不用阿拉伯数字表示,而是用另一种符号体系,就可以看得很清楚了,比如,用十二生肖符号,做这样一一对应。 鼠-0,牛-1,虎-2,兔-3,龙-4,蛇-5,马-6,羊-7,猴-8,鸡-9,狗-十,猪-十一 那么二进制『牛鼠』、十进制的『牛鼠』,改变了符号表示方式,也就看不出和10和2这种客观数字的混淆了。 |
|
谁说二进制写不出2 10不就是么? 啊,你说2不属于二进制? 那10也不属于十进制。 不信我问你十进制哪一位数字是10? 这不是两位数字吗 |
|
因为你允许了十进制下的10用两个数字来编码,却限制了二进制下只用一个数字来编码,对比不公平,自然会发现用更多数字来编码时能表示更多的数字。 |
|
不不不。世界上通行了三种数字体系中,有两款使用十进制,分别是阿拉伯数字和阿语数字。在阿语数字里,既没有2,也没有10。 |
|
因为你没有真的用二进制的观点去使用2进制。你问为什么2进制体系下写不出2这句话,就说明你在形容和思考2进制的时候,使用了一个比2大的(很可能是10)进制体系。 你如果真的在用2进制体系去思考问题的话,2进制其实应该叫10进制。 扩展开来,所有的进制系统其实都是“10”进制。 |
|
“10”只是用位值记数法表示出来的数,并不是独立的一个符号。 十六进制中就有专门的十,也就是“A”,也就是说在十六进制体系下才真正的写出了表示十的符号。 而在十进制中,因为逢十进一,所以也就不需要专门的符号来表示十,而且“10”是两位数,不是一位数。 |
|
因为 2 是 10 进制体系下的。 记住 N 进制是不会出现 N 的,因为逢 N 就在前面加 1 然后 1 后面是 0。 |
|
在十进制体系下写不出一位数的十,但在十六进制体系下可以,就是A。 |
|
十进制是0~9构成,所以是十进制 且逢十进一,且就是and的关系 逢十进一的意思是即将要到十了,就需要进一,比如0、1、2、3、4、5、6、7、8、9、进1,这里的1就要到十位了,那么个位就是从0开始了,所以就是10,10其实又是一个开端了,个位是0。然后是10、11、12、13、14、15、16、17、18、19、又要进1了,这时候十位的1就变成了2,各位的9继续就是0了,就是20了。 二进制是0~1构成,刚好两个数字 且逢2就要进一,所以就是二进制啊 所以二进制是0作为起始位,0、1、10、11、100、101、110、111、1000、1001,这里的二进制就分别代表了0、1、2、3、4、5、6、7、8、9。 |
|
10进制的10,实际是1,0 也就是计算法进面的进位计数,1代表一个十。 而二进制10,那不就是2吗,道理同理。 总结起来都是每位的权重乘以位上的数加起来就是计数值。 你把提问换成另外一个计数,比如罗马计数为什么有 10 , 其值是 X 。这个就不需要写成X0 |
|
|
| [收藏本文] 【下载本文】 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |