| |
|
| 知识库 -> 两性话题 -> 为何全国初中数学平面几何搞那么难,而高中又不咋考?因为高中难度没人能接受?还是说本来这种安排就很扯? -> 正文阅读 |
|
|
[两性话题]为何全国初中数学平面几何搞那么难,而高中又不咋考?因为高中难度没人能接受?还是说本来这种安排就很扯? |
| [收藏本文] 【下载本文】 |
|
为何全国初中数学平面几何搞那么难,而高中又不咋考?因为高中难度没人能接受?还是说本来这种安排就很扯? 关注问题?写回答 [img_log] [img_log] 高中数学 平面几何 初中数学 为何全国初中数学平面几何搞那么难,而高中又不咋考?因为高中难度没人能接受?还是说本来这种安排就很扯? |
|
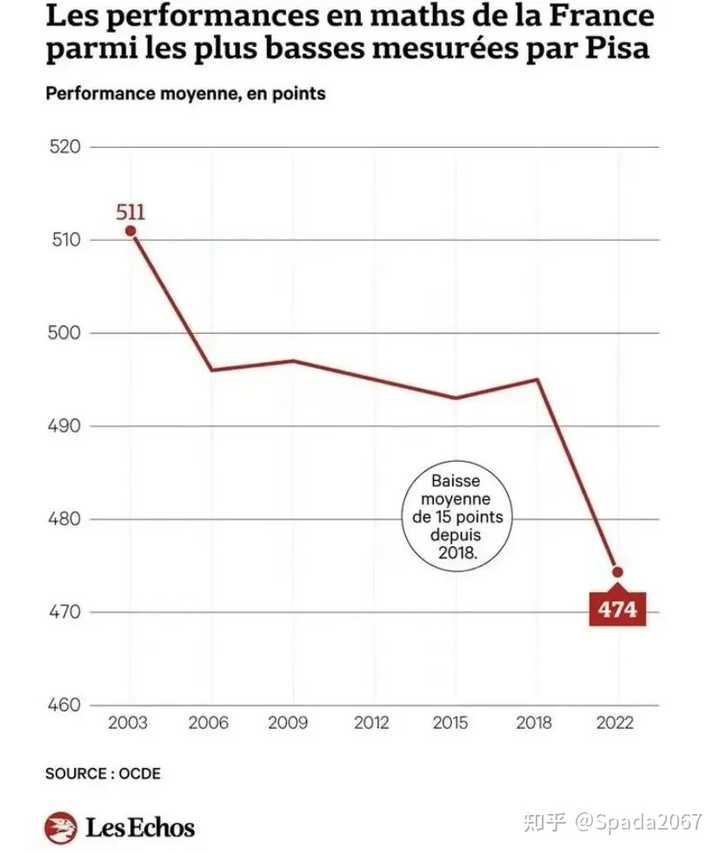
你的这一疑问其实是在数学教学领域一直在讨论的问题,上世纪70年代,欧美国家普遍兴起一场“新数学”运动,这场运动波及美国、英国、法国、日本和中国香港地区。新数学运动的一个核心口号,就是让欧氏几何滚出中学课本。在新数学运动之前,当时中学课本中的平面几何教材,基本上是脱胎于《几何原本》,最为国人所知的教材就是《三S平面几何》。 当时考虑让欧氏几何滚出,源自于几个原因:(1)脱胎于《几何原本》的这些教材普遍存在依赖于直观的问题,与当时数学界的公理化运动不符合;(2)平面几何是已经死亡的数学分支,所有难题(比如三等分角、画圆为方、倍立方体等)已经被解决了,不会再产生新的结论;(3)与后继数学分支关系不大。 基于这些考虑,伴随着新数学运动,欧几里得被从中学课本请出去了,当时这场运动的结果确造成了数学教育的大混乱,比如法国原本是数学大国,可在这场运动之后,大量的大学生失去了最基本的计算能力。邯郸学步,优美的步伐没有学会,连自己本身走路也忘记了。 又是西方各国又不得不把欧几里得又请回来,重新把平面几何编入中学教材。 从《几何原本》发展而来的平面几何,被现代数学诟病 “过度依赖几何直观”,本质是因为现代数学的发展方向是抽象化、公理化、符号化—— 它需要摆脱具体图形的束缚,构建适用于更高维、更复杂空间的通用理论,而几何直观往往只能覆盖低维、具象的场景,存在天然的局限性。 但恰恰是这种 “对直观的依赖”,成了它在数学教育中的核心优势。平面几何通过看得见的图形、可推导的公理、环环相扣的证明,为初学者搭建了从具象感知到逻辑推理的桥梁。学生不需要先掌握复杂的符号系统,就能通过画图、观察、论证理解 “什么是严谨”,这种思维启蒙的价值,是高度抽象的现代数学教材难以替代的。 更关键的是,数学教育的目标和现代数学研究的目标本就不同:前者是培养思维、普及知识、搭建基础,后者是拓展边界、构建体系、解决前沿问题。二者不是对立关系,而是递进关系 —— 很多人正是通过平面几何的直观训练,才具备了理解现代抽象数学的能力。 这里再尝试解释平面几何为什这么难的原因,当然这是我一家之言,大家就听个乐。 先讲个笑话,大家都知道《几何原本》是一本很有名的数学书,但这本数学书除了章节有数字之外,所有命题没有一个提到数字。 我个人觉得这个就是平面几何比较难的原因,因为到今天为止,数学已经发展出来很多很有用的工具,比如实数,向量和矩阵。而平面几何却没有做到与时俱进,把这些数学工具给应用进来。举个例子,就是《几何原本》第五卷的定义五: 定义5:有四个量,第一量比第二量与第三量比第四量叫作有相同比。如果对第一与第三个量取相同倍数,又对第二与第四个量取相同倍数,第一与第二倍量之间依次有大于、等于或小于的关系,那么第三与第四倍量之间也有相应的关系。 这一段相声绕口令一样的定义,实质上就是戴德金分割在比例定义上的应用,我们今天有了实数理论之后,可以把比例定义为(两个比的比值相等,则成比例) a:b=c:d" role="presentation">a:b=c:da:b=c:d 但是由于写作《几何原本》的时代,没有实数定义,有理数(分数)也不是写作 ab" role="presentation">ab\displaystyle \frac{a}{b} 形式(这种记号是15世纪德国数学家鲁多夫所编著的数学习题集,其中应用了分数线),而是分列成两个可以公度的几何量。 如此以来才会造成如何佶屈聱牙的定义,上面那个定义用戴德金分割定义: 如果四个量成比例 ab=cd" role="presentation">ab=cd\displaystyle \frac{a}{b}=\frac{c}{d} ,其比值对应于数轴上一点(此时a,b,c,d为实数),所以对于任意有理数 nm" role="presentation">nm\displaystyle \frac{n}{m} (此处(m,n)=1,m,n互质),有三种可能: \frac{a}{b}=\frac{c}{d}">nm>ab=cd" role="presentation">nm>ab=cd\displaystyle \frac{n}{m} >\frac{a}{b}=\frac{c}{d} nm=ab=cd" role="presentation">nm=ab=cd\displaystyle \frac{n}{m} =\frac{a}{b}=\frac{c}{d} nm<ab=cd" role="presentation">nm<ab=cd\displaystyle \frac{n}{m} \displaystyle \frac{n}{m} <\frac{a}{b}=\frac{c}{d} 补充内容一: 有一位网友不赞同我说的法国中小学数学水平下降,咱们用数据说话: 1、当年就有一个大新闻,法国的教育改革之后,数学不再是必修科目,学生从高中一年级分流,导致许多学生高二以后就不学习数学了。据统计,2021年只有37%高三学生继续选择数学科目。 2、教学时长缩减:改革后中学数学教学时长大幅下降(有报告称下降38%),加剧了学生数学基础薄弱的问题。 3、学生数学能力断崖式下跌:基础教育质量面临严重挑战,初中生数学和阅读成绩大幅下降。在经合组织OECD的PISA测试中,法国初中生数学成绩垫底,近十年来更是断崖式下滑。 |
|
|
4、“数学人才荒”的担忧:就在全世界都在人工智能领域追求创新的时候,由于法国缺少数量足够大的“中高端数学工程人才”,在人工智能核心技术上的竞争力明显弱于美国和中国。 不是说法国没有精英数学家,法国作为数学大国,以及Fields奖得主数量位于世界前列,有大量顶级数学家聚集于X、ENS、Télécom Paris,但是由于法国的数学文化偏“纯粹与优雅”,工程数学长期被视为“次一等”,这些人擅长抽象讨论,但不耐烦于应用数学。 总结 法国的数学改革因措施过于激进,导致学生数学素养普遍下降,对国家科技创新能力造成了潜在的重大冲击,形成了深刻的社会与教育之痛。 补充内容二:法国新数学运动在取消平面几何之后,为什么造成学生的计算能力下降 法国“新数学运动”在弱化乃至取消传统平面几何教学后,确实出现了学生计算能力与基本数学技能下降的现象,这是不争的事实。当然其原因并不是“几何本身教计算”,而是由一系列教学结构性变化叠加造成的。核心原因可以从以下几个层面理解: 1、传统平面几何虽然不直接教四则运算,但它持续、隐性地训练了计算能力: 求长度、面积、比例 → 大量数值计算 相似三角形、比例定理 → 分数与比例运算 勾股定理、面积转化 → 平方、平方根计算 学生在解决几何问题时会被潜移默化,被迫反复计算,而且这些计算有明确意义和目标,不是机械练习。取消几何 之后,学生失去了“有情境的计算训练”。 2、新数学过度强调抽象化、结构化、符号化,弱化了计算“熟练度”训练(也就是刷题) 新数学运动的核心理念是: 数学 = 结构(集合、映射、代数结构) 结果是:大量引入集合论符号(∈、∪、∩)和抽象代数语言 减少了:重复的算法练习,心算与笔算训练 但计算能力的形成高度依赖重复与熟练,而不是“一次性理解”结构。学生表面上“懂得概念”,实际却算得慢、算不准。 这样的学生我们也见过,满嘴相对论,不愿意踏踏实实计算。 引用一段法国数学家迪厄多内在《无穷小计算》序言里面的话: “现在的大学生不再会计算了”,常常听到物理学家和工程师像这样抱怨当前的数学教学.必须承认这种抱怨是有理由的.当我们看到一位理学院二三年级的大学生花了十分钟才费力做出一次变数代换或分部积分时,就不能不感到十分厌烦,特别是(情况有时是这样)当这位大学生还自以为是说出一些他所不懂的无用的废话,来为他的无知和笨拙加盐添醋的时候。 3、几何提供了几何直观的“认知支架”,支撑数感发展 平面几何有一个关键作用:把数和运算“可视化” 例如:面积 = 数的乘法的几何解释,比例 = 线段长度的对比,分数 = 图形分割 取消几何后:数学变成符号之间的操作,数不再“有形”,只能靠记忆规则,从而导致学生的数感变弱:对结果大小缺乏直觉,容易出现低级计算错误却无法自检 4、证明训练消失,削弱了“步骤意识” 传统几何证明训练了: 严格的步骤顺序,中间结果的检查,条件—结论的逻辑链 而计算能力不仅是“会算”,还包括:按步骤操作,不跳步,检查合理性 新数学中:证明形式高度抽象,更像“符号操纵”而非“推理链条” 学生在计算中更容易:跳步骤,忽略中间检查,对错误不敏感。 总结一句话 法国新数学运动取消平面几何,并不是“少了一门内容”,而是切断了计算训练、数感培养、步骤意识和直观理解之间的关键纽带,导致学生在“懂数学语言”的同时,失去了把数学算出来的能力。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
我记得人教版教材的主编对初中几何的评价是思维体操,我觉得这个评价极为精准。 单纯从初高衔接的角度说,平面几何对未来的数学学习帮助有限,但是从培养逻辑思维的角度看,没经历过平面几何的训练,高中数学物理学习都会遇到很大障碍。从我国的基础教育看,1-9年级,也只有平面几何在进行逻辑思维训练,但是强度也不高。 以物理为例,高中阶段难度直接拉满,哪怕是教育大省,百分制下高考平均分也就30-40之间,很大的问题就在学生逻辑思维能力低下,物理和数学建模能力极差,也没有多少逻辑分析能力,大部分学生只会机械背诵,看到数学证明题直接抓瞎。初中平面几何学的好的孩子,高中数学物理的学习肯定会轻松点。 初中平面几何的现在的问题在于,中考为了区分度,加上大家一起军备竞赛,搞点稀奇古怪的所谓创新题,这些是不是数学题真的两说。还有些比较偏门的东西,类似费马点,阿波罗尼斯圆,胡不归等等,在没解析几何工具之前,处理这些玩意真的费脑子。偏偏反证法这种特别重要的东西,初中变成了选学,也不考,训练逻辑思维,肯定要懂反证法啊。 整个初中平面几何的教学考试,给我的感觉就是主打一个基础的学的不够,难题又难度过高,有点扭曲。 |
|
我高考数学142,全国一卷(大题是圆锥曲线+导数 三角、数列在第一、第二道大题)。说句真心话,你按初中中考数学给我出一套150分卷,挑我人生中考试能力最强的一个时刻,我大概率都上不了120 高考数学是可以刷题刷出来的(只要不是葛军出题,以及不要最后一题搞数列),极值点平移 二阶导放缩 泰勒放缩,圆锥曲线更是了,圆锥不考脑子,只考计算,套路相当固定,联立方程韦达定理,练多了就熟了; 初中中考数学,连两条辅助线的圆几何,你不告诉我答案让我猜,我猜一年都猜不到那种连法,你让我再刷题,我顶多能做连一条辅助线的圆几何,两条的真猜不出来;最后一道二次函数动点解,我当时怎么算都不对,后来一看答案好家伙,一个分式,分母分子都是根式+整式,分子的长度写出来快占一行,那个答案,你提前让我先把这道题做一遍,再进考场,我都算不出一模一样的 总结一个:高考数学是学杜工部写诗,初中数学是学李太白写诗(尤其圆几何) |
|
因为平面几何(欧式几何)能很好地训练思维灵活性和逻辑能力,也就是各种“因为…所以…”的推理。虽然解析几何可以完美取代欧式几何,但这种取代只是工具层面的,平面几何这种利用很少很简单的公理,就能推出大量结论的领域,对于早期学习阶段训练思维的作用还是很难被替代的。 另外,虽然高中的平面几何几乎都是用坐标化的向量、方程求解,但高中的立体几何还是专门学习欧式几何的知识的,并且时不时地会在高考题中出现。坐标化虽然可以节省很多分析推理,但计算量通常较大,很多空间关系的证明和推理用欧式几何会简便得多。 欧式几何中经常需要添加精妙的辅助线,这也是欧氏几何训练思维灵活性的特点,而解析几何通常不需要。添加辅助线并不是多了条件,而是让原本就存在的“隐藏条件”显现出来。 解析几何通过建立坐标系,把空间内的点坐标化,坐标表达了点的全部信息,那么由点构成的曲线、曲面等图形,它们的信息也都蕴含在相应的方程以及参数里,通过方程和参数之间的关系,就可以找到点(元素)或者图形(集合)之间的关系,所以不太需要添加辅助线。 欧氏几何没有建立坐标系,点和图形的特点和性质需要通过相互之间的关系来体现,如果图形上没有直接的联系,那么就很难明确地指出它们之间的关系,所以经常需要添加辅助线。 举个最简单的例子:平行关系。欧式几何中,要证明两条直线平行,通常是通过作一条它们的交线,证明同位角相等,或者证明它们都平行于第三条直线,其他证明方法的原理也基本都是这样,如果没有这第三条直线:交线或者平行线,就难以证明它们平行。 解析几何中,只要求出两条直线的方向向量,不需要任何“第三者”的介入,仅仅上比较它们自身的特点,就可以证明它们平行。 另外,诸如垂直、点到直线的距离、点到平面的距离、平行线间的距离、平行的直线与平面给间的距离、直线之间的夹角等等很多概念,解析几何的定义也远比欧式几何要清楚明确得多。 尽管解析几何有很多优点,但是欧氏几何与人类的直觉更加贴近,很多定理也足够方便好用,因此不需要非此即彼、舍此就彼,两方面结合起来各取所长会更加有效。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
平面几何不是为难人,而是让别个学生养成一种思考的习惯,完整的逻辑。 几何只有寥寥几个公理,其余所有内容都可以聪几个公理推导而来,这就是数学逻辑的魅力。 初中是嚷学生感受学习这个过程,所以题目不会太难,辅助线不会太多。 如果高考也考就坏了,平面几何的难度可以上天!而且有了解析几何后平面几何不那么重要了,很多问题可以用解析几何解决。 |
|
|
| [收藏本文] 【下载本文】 |
| 两性话题 最新文章 |
| 如果去医院挂号掏耳朵医生给掏吗? |
| 为什么免签后越来越多的外国人来中国看病? |
| 什么是媚眼如丝,你见过吗? |
| 杭州两只大熊猫相继死亡,均因消化道急腹症 |
| 为何一些几乎必死的晚期癌症患者会选择花费 |
| 碳水这个词是怎么变得到处都是在说的? |
| 作为40岁的女人,你现阶段是怎样的状态? |
| 如果把现代美女写真拿给明清古人看,他们会 |
| 媒体称「日本大医院非患者想去就能去」,这 |
| 男人为什么那么好色? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |