| |
|
| 知识库 -> 科技 -> 美国斩杀线为什么刚好在1/e附近? -> 正文阅读 |
|
|
[科技]美国斩杀线为什么刚好在1/e附近? |
| [收藏本文] 【下载本文】 |
|
多个调查说明美国社会的斩杀线差不多是37%,也就是1/e附近。(搬运一个数据来源:美联储报告显示37%的美国人拿不出400美元应急现金。) 太诡异了,… |
|
用初等数学简单解答就是: limn→∞(1−1n)n=1/e≈0.3679" role="presentation">limn→∞(1?1n)n=1/e≈0.3679\lim_{n\to\infty}\left(1-\frac1n\right)^n=1/e\approx 0.3679 如果n个人完全随机分n块蛋糕,当人群n足够大时,一个蛋糕都没有的人的比例大约为1/e 也就是说西大完完全全遵循弱肉强食的准则,根本没有二次分配。 不愧为完美资本主义帝国,实际数据接近理论值。 |
|
因为e分之1就是所谓的“倒霉常数”。 就好像你在游戏里抽卡,百分之一出货率下你抽一百次没出货,你会认为是自己倒霉;万分之一出货率下你抽一万次没出货,你也会认为自己倒霉。 你用计算器按一下这两者的几率就会发现很接近(四舍五入均为约37%)。那么你继续带入一百万、一亿、一百亿。。。就会发现几率无限逼近e分之一。 没错,e分之一就是(1-1/n)^n的极限。 这就是随机系统自发的趋势:当成功几率和机会次数互为倒数时,约有37%的人会倒霉。 政府不有意管人民也不故意害人民时,这就是自然的常数,这就是天理。 现在你可能想问:那么咱们有没有办法不让那么多人倒霉啊? 当然有。 不让成功几率和机会次数互为倒数就可以了。机会的次数是成功率倒数的2倍,倒霉的人就只有13%了;提高到3倍,倒霉的人就只有不到5%了;提高到4倍,倒霉的人就不到2%了;提高到5倍,倒霉的人就不到1%了。 在你倒霉(用完天经地义的机会次数之后还没能成功维持生存)时多给你几次机会——这就是我国政府在做的事。 而在你倒霉(用完天经地义的机会次数之后还没能成功维持生存)时直接结束游戏——这就是美国政府做的事,也就是所谓的斩杀线。 天理就规定了37%的人要倒霉,而我们的政府就是为了人民在逆天而行。 |
|
刚刚我脑子里忽然冒出来一个念头:既然是大数定律,中国的人口基数更大,理论上这个1/e 应该更明显才对。 我们来查一查: 2023年,中国乡村常住人口 4.77 亿,占总人口的 33.8%。 再加上城市里的调查失业率(约 5%),折算到总人口里大概是 3% 左右。 33.8% + 3% ≈ 36.8% ≈ 1/e。 嗯?? 这也太精确了。 好在我们有土地集体所有制+转移支付+底保等等一系列的制度,这些人能以极低的功耗运行在乡村。 我愿称之为“中国锁血线”。 换句话说,如果有一天,诸位农村老家的那套宅基地如果被盯上了…… |
|
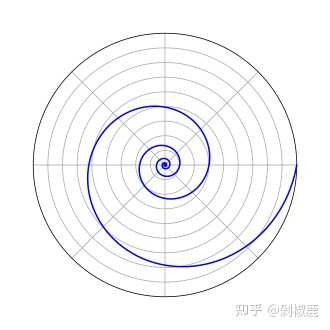
注意力非常惊人,堪比拉马努金。 多说一句,这个统计数据接近37%多半是一种巧合。 因为拿不出400美元这个数据每年都在变,且不见得400美元就是斩杀线。 但是很多情况下出现37%跟1/e倒真是有关系。 要了解这个,我们先要来了解一下,什么是自然底数e? e≈2.71828182845904523536... e是一个超越数,是指一种不可以作为某个代数方程的根的实数或复数。 e这玩意看起来一点都不“自然”,它到底是什么自然的底数? 别慌,我们画个方程: y= e^x 嗯,平平无奇嘛,不着急,我们把它换成极坐标: \\在极坐标中,x = \cos(\theta) 和 y=sin?(θ),因此: sin?(θ) = e^{\cos(\theta)} |
|
|
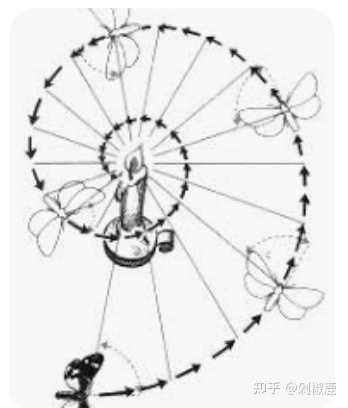
这个图像眼熟了一些吗? 是不是很接近自然界的各种螺线? 大自然的对数螺旋 在几种自然现象中,你会发现几乎是对数螺旋的曲线。比如: 鹰找到猎物:他们最清晰的视野与他们的飞行方向有一定的角度。这个角度与对数螺旋的夹角相同。 |
|
|
昆虫到光源:它们习惯于将光源与飞行路径保持恒定角度。通常,太阳(或夜间物种的月亮)是唯一的光源,以这种方式飞行将导致几乎直线。 但是人造光源离得太近,虽然它们夹角恒定,但是会导致越飞越近造成飞蛾扑火的现象。螺旋星系的臂。我们的银河系,有几个螺旋臂,每个螺旋都大致是一个对数螺旋,螺距约为12度。 |

|
|
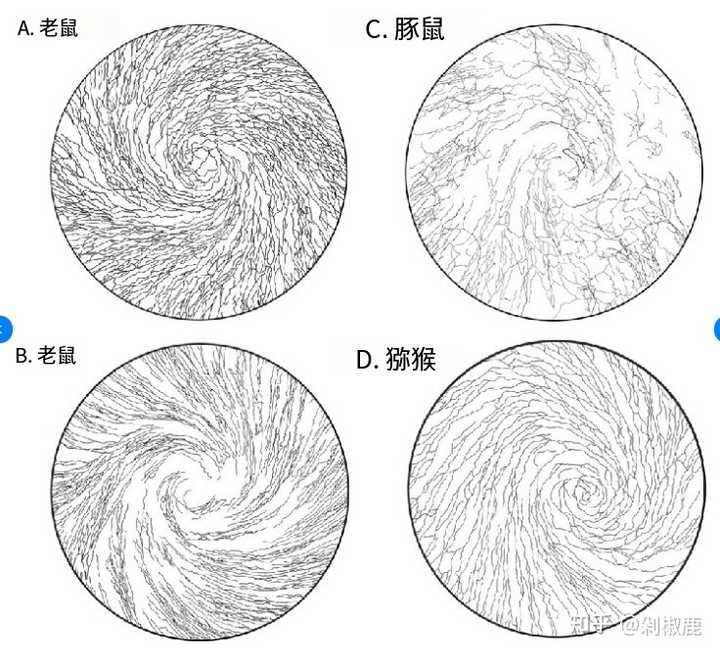
角膜神经 (这是几种不同动物的角膜神经,以对螺旋模式在角膜的浅表皮层附近终止)。 |
|
|
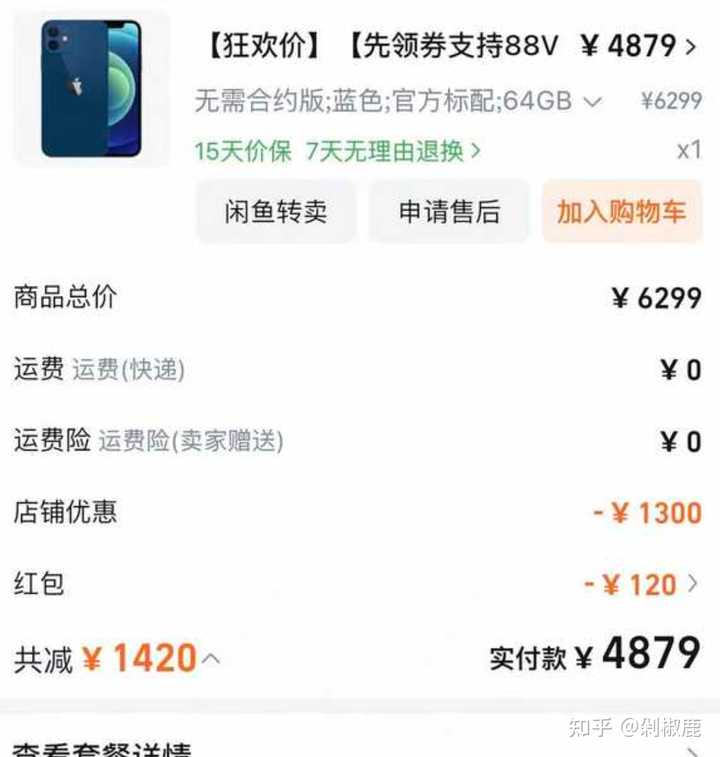
热带气旋,例如飓风。许多生物结构,包括软体动物的壳。 由此可见e在自然界存在非常广泛,但是这还不是它叫做自然底数的原因。 e是这样定义的: 当n趋近于无穷大时,(1 + 1/n)^n的极限,即e = lim_{n→∞} (1 + 1/n)^n 它之所以叫自然底数,源自它那古希腊哲学一般的形式美感:e 的一个重要性质是它是唯一一个使得其导数等于自身的数。也就是说: 函数 f(x)= e^x的导数 f′(x)也等于 e^x 这使得它在微积分和数学分析中非常重要。 简单来说,我们可以认为e的本质是连续不断的增长(或衰减)。 现实世界中,极少有事情是像光电效应一样到一定数值才激发,大多数事情(细菌分裂、谣言传播、资产增值)是每分每秒都在发生的。所以用到e的地方会很多。 比如假设你有 1 块钱,银行很大方,年利率 100%。 一年结一次息: 年末你有 2 块钱。 半年结一次息,到了年底你就有 : (1+1/2)2=2.25(1+1/2)2=2.25 每天结一次息,到了年底你就有 : (1+1/365)365≈2.714(1+1/365)365≈2.714 要是银行用电脑给你每秒、每毫秒、连续不断地结息呢? 那到了年底你就有 \lim_{n \to \infty} (1 + \frac{1}{n})^n = e \approx 2.71828... 这就是这就是连续复利公式的由来 : A = P ? e ^r t 它告诉我们,靠“利滚利”的频率来增加财富是有天花板的。 你在一年的时间里不能通过无限次地结算利息来把 1 块钱变成 100 万,宇宙的极限锁死在了 2.718 倍左右(在 100% 利率下)。 那么,复利增长可以用e,价值衰减能不能用e呢? 也是可以的。 我经常在网上买二手的东西电子产品,会发现一个有趣的现象。 所有新的电子产品,只要拆开激活使用就开始贬值,不管你是用一次还是十几次,都会跌一个让你肉疼的价格,大几千的新机器,使用几次后不是你降价几十或者100块钱就能卖出去的,比如我买了一个12月1日才激活仅使用过一次的无人机,原价1500,卖家最终1200出售。 大多数电子商品使用一年左右,价格会跌到原价的一半以上。 但是你这个时候买二手的再用两个月,价格不会变成原价的1/4,而是依然能以差不多始发价半价卖出去。 其实仔细算算并非一半,而是接近36.8%,也就是e的倒数1/e。 举个例子,你今天买了一个一万的新苹果手机,但是你打开激活的一瞬间就开始贬值了。 你支付的购置税、保修、新手机溢价等费用,在转手时没人会考虑。 这部分贬值是即时且剧烈的,通常在第一个月就能损失原价的 10% 到 20% 甚至更高。 也就是说不管你是开了一周还是一个月,要卖的话估计都要有10%左右的跌价损耗。 过了这个剧烈衰减期间,后面价格的变化就按照指数衰减: V(t) = V_0 \cdot e^{-kt} V指的是商品的初始价值(比如新车的购买价)。 k衰减率常数。这个值越大,商品贬值越快。 这个公式意味着你买的商品的价值不是固定数量的减少,也不是固定百分比的减少(比如每年都减少几千块钱),而是每单位时间减少一个固定百分比。而正是这种“连续复利式”衰减的数学基础。 假如我们取k=1,单位时间一年,也取做1。 那么我们的苹果手机一年后会贬值到原价格的1/e,就约等于36.8% 当然,现实生活中苹果贬值没这么快,这里单位时间要久一点。 我这里找了一个我2021年买的苹果12: |
|
|
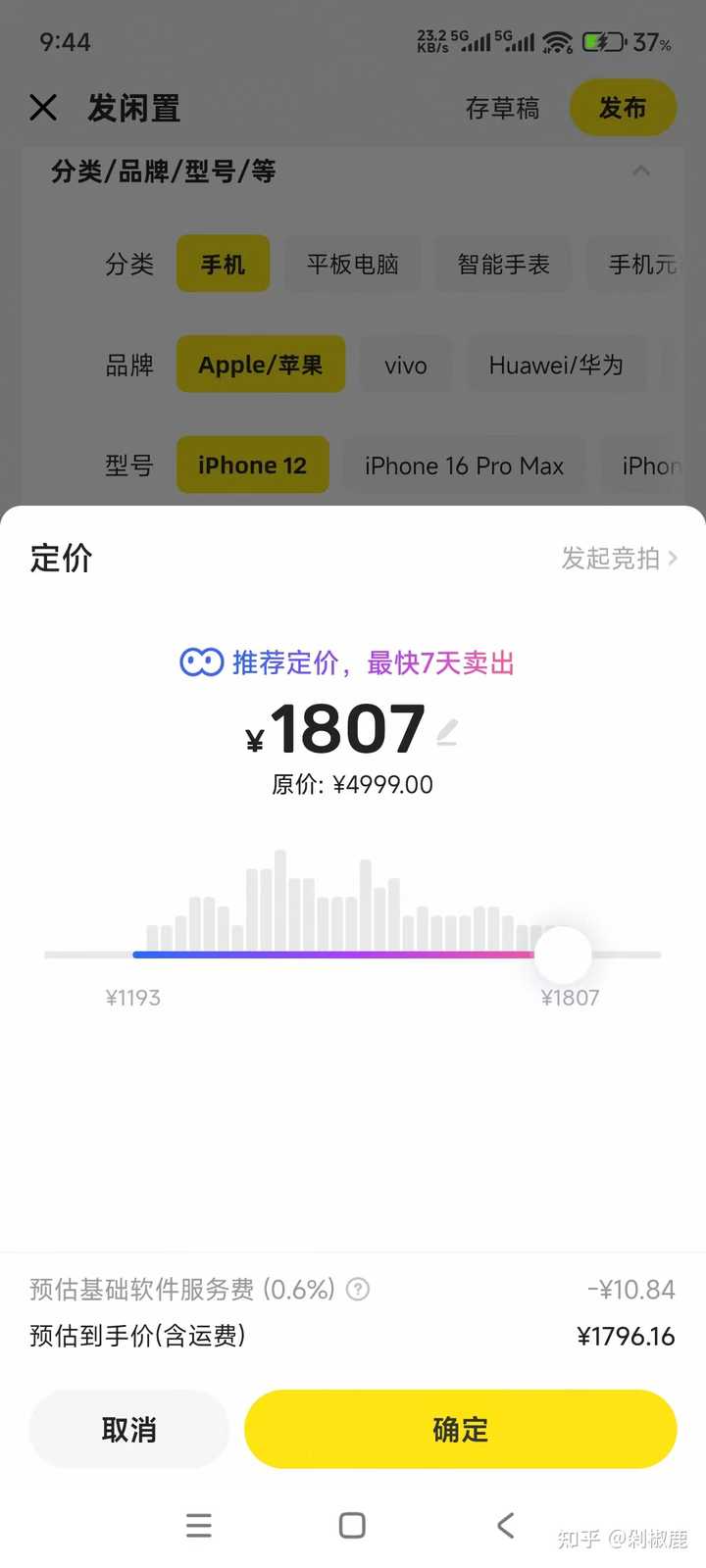
当时的价格是4879,如果我现在放到二手平台能卖多少呢? |
|
|
最近的最高成交价是1807左右(且品相完美),意味着高于这个价格可能就很难卖出了。 那么这个价格就是1807/4879≈37% 看,我们的37%出现了! 很有趣是吧。 只要增长或者衰减是连续的,我们总是很容易的能找到e能见缝插针的地方。 所以回到我们的斩杀线上。 37%的概率恰恰是数学上的最优停止理论。 这其实跟苏格拉底捡麦穗是一样的概率。 相传,苏格拉底的三个弟子曾向他请教如何找到最理想的伴侣。 苏格拉底并未直接回答,而是让他们走进一片麦田,要求他们分别从中选择一支最大的麦穗,且只能摘一次,不能回头。 第一个弟子刚走几步就摘了一支自认为最大的麦穗,但后来发现后面还有更大的,于是遗憾不已; 第二个弟子则一路犹豫不决,最终空手而归; 第三个弟子则吸取前两人的教训,他先观察麦穗的大小,分出大、中、小三类,然后在最后三分之一的路程中果断选择了比参照物更大的麦穗,最终满意而归。 假设一共有N个麦穗(可以预见,N这个数字很大)如果你随机选,选中的概率是 1/N 如果你把所有麦穗都看完,你只能选最后一个,但它未必是最大的。 数学家的策略(37%法则): 你应该把前 37%(准确地说是 1/e)的数据作为“观察样本”。 对这前 37% 的麦穗,无论多大,统统不要,但记下它们中最大的一个X 从第 37% 个麦穗之后开始,一旦遇到一个比X大的麦穗,立即采下来,能确保你采的麦穗在策略上是最大的。 数学证明,使用这个策略,你选中最大麦穗的概率,竟然也刚好是 37%(准确地说是 1/e)左右。 这说明37%就是在不确定性面前,人类能达到的数学极限。 也就是说,斩杀线37%可能确实是巧合,但是如果我们真打算淘汰一些人,留下那些比较好,那么淘汰最底下的37%可能就是社会达尔文丛林里给出的终极答案了。 抽卡也是同样的道理,当样本量足够大(趋向于无穷大)时,如果你有 1/n的概率中奖,尝试 n次,你一次都中不了的概率,就是 1/e,也就是 36.8%左右。 也就是说1/100的抽中概率,你抽100次一次也不中的概率居然高达36.8%,正因为如此,游戏厂商才要设置保底,免得你卸载游戏。 自然底数e就是这么神奇啊~ 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
突然有一个令我升起一阵恶寒的想法。 如果美国37%的斩杀线真实存在,并且推论得出这是整个美国社会共谋的结果。那么美国人能对身边数量庞大的、具体的homeless熟视无睹,不把他们当做有尊严的人。 那么,他们会把远隔千里,大洋彼岸的、抽象的人类,看做什么? 我们如果用过往的以己度人、换位思考的方式去理解他们,是不是产生了偏差? |
|
|
| [收藏本文] 【下载本文】 |
| 科技 最新文章 |
| 为什么有些人不敢使用微信? |
| 作业帮 iOS 版应用被曝存在假卸载按钮设计, |
| 你认为稀土是中国手里的终极王牌吗? |
| 如何看soul这个软件? |
| 如何看待FARS批量制造100篇论文? |
| 为什么有些用户宁愿看盗版,也不愿为正版视 |
| 英政府拟强制中资桥接芯片巨头FTDI出售80%股 |
| 如何看待姚班大神陈立杰官宣入职 OpenAI? |
| 微信有多傻逼? |
| 如何看待「斩杀线」概念的出现及其影响? |
| 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |