| |
|
| 知识库 -> 科技 -> 如何理解 DeepSeek 最新提出的 mHC 架构? -> 正文阅读 |
|
|
[科技]如何理解 DeepSeek 最新提出的 mHC 架构? |
| [收藏本文] 【下载本文】 |
|
mHC: Manifold-Constrained Hyper-Connections |
|
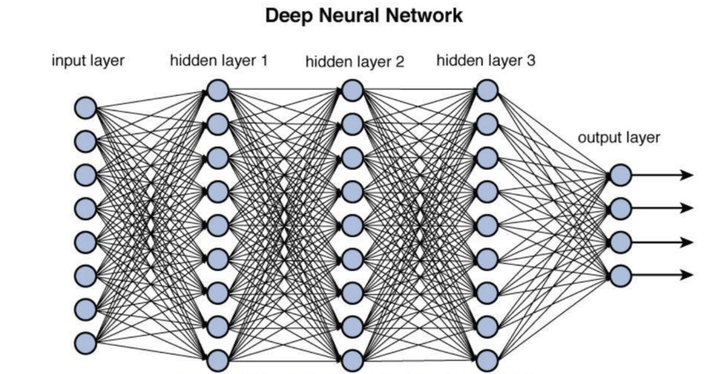
我尝试着用让你爷爷奶奶都能理解的方式来描述mHC架构。 如果想理解mHC,先要知道HC(Hyper-Connections);如果想理解HC,先要知道Residuals(残差);要理解Residuals,先要知道深度神经元网络(Deep Neural Network)。 所以,有这样的一个认知递进: Deep Neural Network -> Residuals -> HC -> mHC 好吧,还是有点复杂,可能你爷爷奶奶没兴趣听下去,但是你可以继续看下去,在本文结尾有直接给爷爷奶奶解释的版本。 什么是深度神经元网络(Deep Neural Network,DNN) 这个太多介绍了,在这个问题中,只需要知道DNN是由很多层构成的,因为层数多,所以Deep,而且,每一层都以表示为一个函数 y=f(x)" role="presentation">y=f(x)y = f(x) x是这一层的输入,y是这一层的输出。 |
|
|
可以想想,当很多f函数叠加在一起,就可以表达复杂的函数关系,这也是DNN比较强大的原因。 但是,原本的输入,在每一层的传递过程中,特征会逐渐衰减,这给机器训练带来很大挑战。 打个比方:在一个大型公司里,CEO下达指令给CTO,CTO下达指令到VP,VP下达指令到Director,Director下达指令到Team Lead,Team Lead下达指令到基层组员,在这个指令传递链条中,原本CEO的想法会被模糊化,很容易被曲解,最后基层组员所理解的CEO最初想法可能大相径庭。 于是,有了——残差。 什么是残差(Residuals) 残差的概念是,把上面每一层的函数做一下修改,变成这样: y=f(x)+x" role="presentation">y=f(x)+xy = f(x) + x 也就是,每一层给下一层的输出y,不只是这一层操作过的f(x),而且包含这一层的输入x。 |

|
|
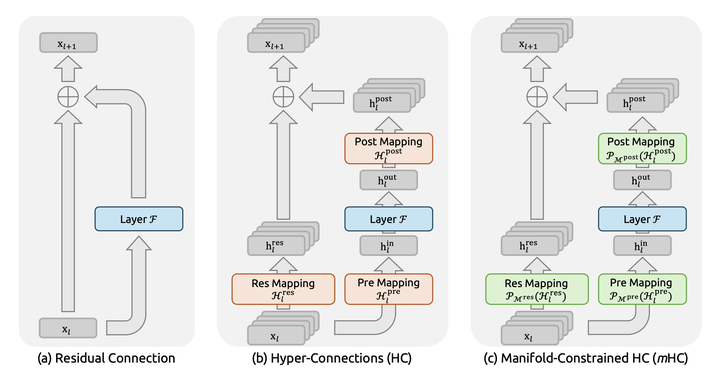
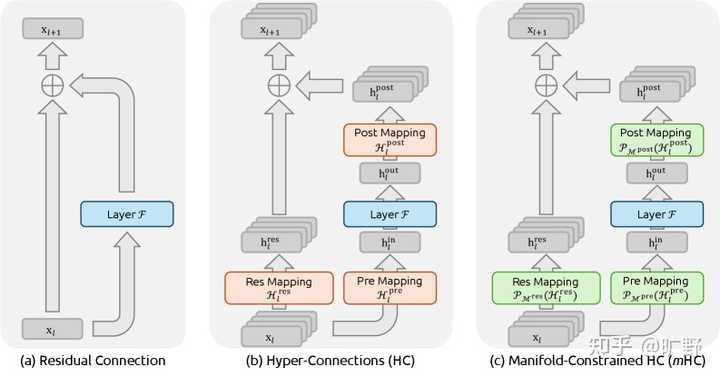
还是拿大型公司打比方: 现在CEO给CTO下了指令,CTO在理解了CEO的指令之后,除了把自己的理解给下一层的VP,还把CEO原本的指令一起给了VP,这样VP不光拿到了CTO的指令,还有CEO原本的指令。 同样,CTO给VP下达指令的之后,VP不光给Director自己的理解,也把CTO给的指令传给VP ...... 依次类推,VP、Director、Team Lead直到基层组员,不光能够直到上一层理解的指令,还知道上上一层的指令。 这样,每一层获得的信息更大,避免信息衰减,原本CEO的想法更保真地传递给基层。 什么是HC(Hyper-Connections) 在DeepSeek论文里的这张图,中间的部分就是HC,但这是简单起见只展示了一层HC的架构,实际上HC可以跨越多层。 |
|
|
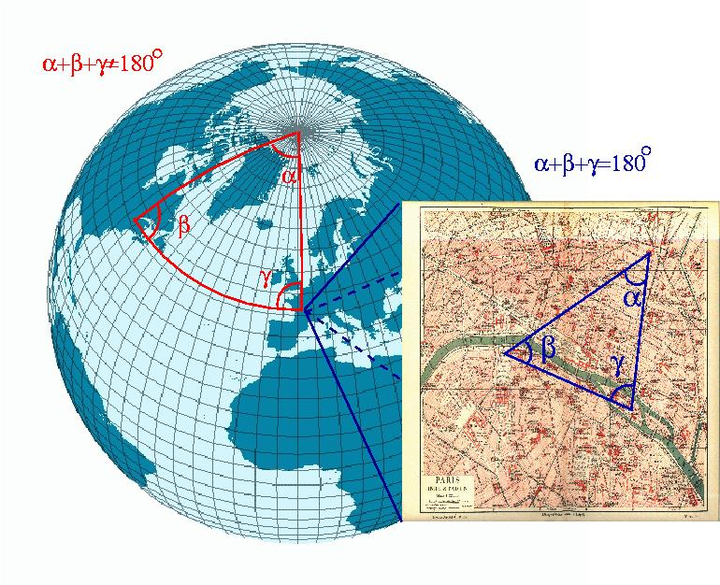
还是拿大型公司打比方: 为了进一步提高指令传递有效性,不只是越级传达,还可以有更多样的指令传递渠道。 比如,CEO传递给CTO的指令,CTO可以选择性传递,技术无关的信息,CTO就降低权重传递给下面的VP,和技术相关的信息,CTO就增加权重传递给VP。 CTO甚至还可以选择把重要指令直接越级传递给Director甚至Team Lead层,只要他觉得这非常重要。 毫无疑问,HC是Residuals的强化版,预期可以产生更保真的信息传递。 什么是mHC(Manifold-Constrained Hyper-Connections) 要理解mHC,先要理解什么是Manifold(流形) 什么是流形(Manifold) Manifold是一个数学概念,用最简单的化描述就是:近看是N-1维的东西,实际是N维东西的投影,这就是N维流形。 举例来说,地图就是流形,因为地球实际上是圆的,地形也是有高低起伏的,是三维世界的东西,但是,看地球上的局部地区的时候,可以看成是二维的地图。 |
|
|
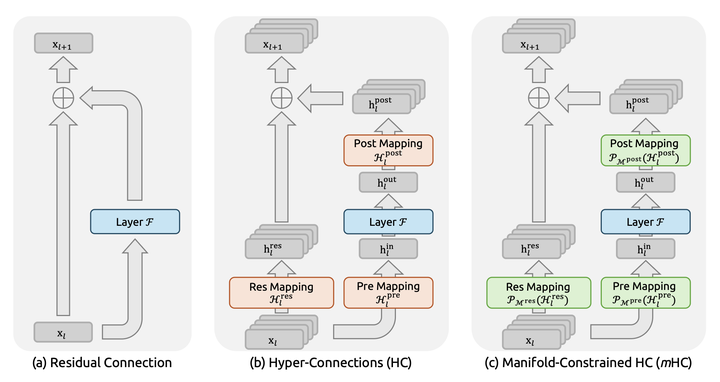
重点就是,虽然我以二维方式表达三维地球并不是全貌,但是看起来也能有我这个维度需要的所有信息,可以看得懂。 对于神经元网络中的数据空间,也存在这种N维数据可以在低维度看起来是连续平滑的流形。 那么,什么是mHC 我们再来看DeepSeek论文中的图,最右侧就是mHC,对比HC就很清楚了。 |
|
|
还是拿大型公司来打比方。 在HC状态下,层级之间的壁垒是被打破了,信息传递更加充分了,但是容易带来不稳定性。 设想一下,CEO直接给一个编程的基层组员下达指令,这个组员肯定会很疑惑,大家不在一个层面上啊,你CEO掌握的是公司方向,我基层程序员解决的是具体bug,换句话说,CEO的流形和基层组员的流形根本不搭。 mHC就是给HC施加一些约束,比如,CEO的KPI之一是『提高产品质量』,那这个流形基层程序员可以看懂,对应于『减少Bug』,可以看得懂;但是,CEO的另一个KPI是『扩大融资额』,这就和基层程序员的工作完全不相关,看不懂啊,就不要听CEO哔哔这些了。 CEO有自己的世界观和地图,但是这种流形如果无法被其他层理解,那就不要做为那一层的参考了,或者,要换成那一层能理解的样子,这样才有参考意义。 总之,mHC就是给HC一些约束,让多样的信息流动也有一些约束,避免不稳定性。 写在最后 这次DeepSeek只是一篇论文,并没有对应的模型发布来验证这个想法,后续应该能看到产品发布,不过,这个『Deep Neural Network -> Residuals -> HC -> mHC』演化如此自然,感觉就是水到渠成。 值得一提,Residuals、HC和mHC全都由中国人贡献! 最后,给出你爷爷奶奶也能理解的mHC版本: 就像织毛衣一样,以前手工织毛衣只用一根线,效率不高。然后,我们发明一种机器,使用多股线一起编织(HC),这样效率就高多了,但是容易多根线头之间容易缠绕。现在用mHC方法,添加了一个智能理线器来防止线缠绕。这样一来,我们织出的毛衣更加结实耐用,而且更加美观。 你学会了吗? 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
DeepSeek 这群人是真的闲不住啊。 残差连接,这个从 2015 年 ResNet 开始统治深度学习界的基础范式,十年了,就没人敢动它。结果 DeepSeek 直接上手了——基于字节跳动 2024 年提出的 Hyper-Connections (HC) 思路,搞出了一个"流形约束版" mHC。 不得不说,这波操作属实有点猛。 |
|
|
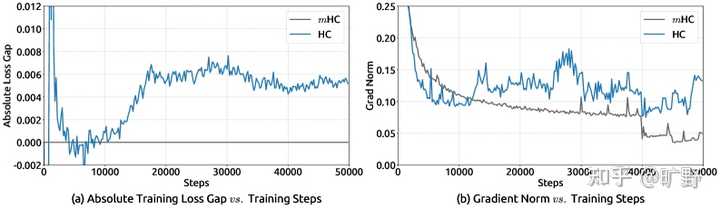
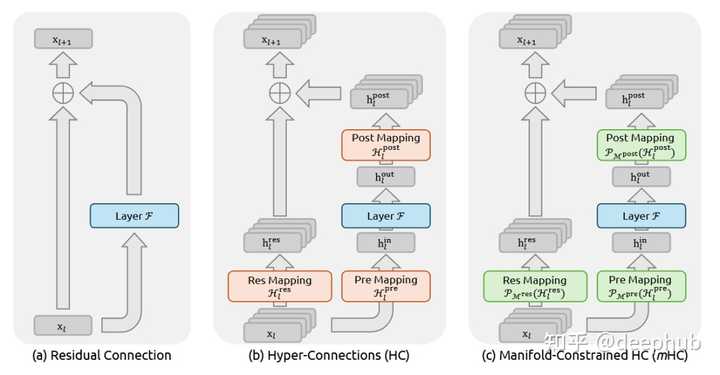
残差连接、HC 与 mHC 的结构对比。mHC 的关键是在残差映射上加入“流形投影”约束,从而在拓扑更复杂的同时保持训练稳定性。先搞清楚问题在哪 在聊mHC之前得先理解HC到底解决了什么问题,又制造了什么新问题。 传统的残差连接,公式大家都熟悉得不能再熟悉了: \mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l) \\ 就这么个简单的东西,支撑了Transformer这十年的繁荣。为什么?因为恒等映射这个性质实在太好了——信号从浅层直接传到深层,不修改、不衰减、不放大。梯度反传的时候也是如此。 但HC觉得 你这残差流太窄了,我给你扩展成n条流,再用可学习的矩阵去mix它们。 这想法确实很好。你想啊,原来的残差连接就是个 1×1 的"矩阵",其实就是个标量 1,现在变成 n×n 的可学习矩阵,拓扑复杂度一下子就上去了。而且关键是——不增加 FLOPs,只是多了点小矩阵运算。 HC在小规模实验上效果确实不错。但随之而来的也有问题: 规模一上去就炸了。 论文里有个很有意思的图(Figure 2),27B 模型训练到 12k step 左右,HC 的 loss 突然飙升。与此同时,梯度范数也开始疯狂震荡。 |
|
|
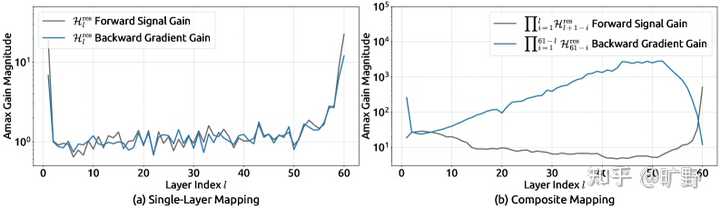
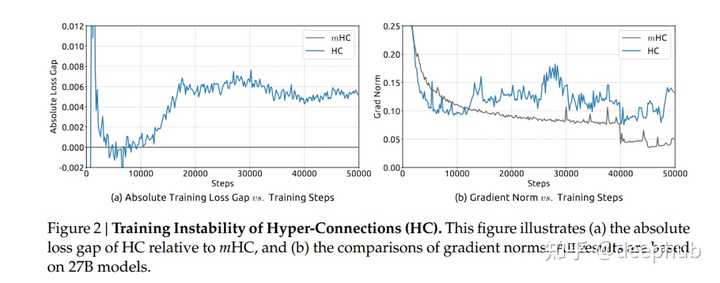
HC 在 27B 规模下出现训练不稳定:相对 mHC 的 loss gap 在约 12k step 附近突增,同时梯度范数剧烈波动。 为什么会这样?原因其实不难理解。 当你把单层的残差映射矩阵 \mathcal{H}_l^{res} 连续相乘 L 层之后: \prod_{i=1}^{L-l} \mathcal{H}_{L-i}^{res} \\ 由于这些矩阵是unconstrained的,这个复合映射可以往任意方向发散。论文测量了一个叫 "Amax Gain Magnitude" 的指标——这个值在 HC 里飙到了 3000。 |
|
|
HC 的残差映射在单层与跨层复合后会显著偏离恒等映射,Amax Gain Magnitude 出现极端峰值(可达 3000 量级),对应前向信号与反向梯度的爆炸/消失风险。 这个信号在残差流里被放大了 3000 倍。在大规模训练中,这就是爆炸的前奏。 mHC的核心——为什么偏偏是双随机矩阵? 好,问题搞清楚了。现在 DeepSeek 的解法来了。 mHC 的核心思想给个省流版就是: 把残差矩阵 \mathcal{H}^{res} 约束在双随机矩阵构成的流形上。 等等,什么是双随机矩阵? 简单点看就是一个”特别均匀”的矩阵——所有元素都是非负的,而且每一行加起来等于 1,每一列加起来也等于 1。 比如一个 3×3 的双随机矩阵,它可能长这样: |
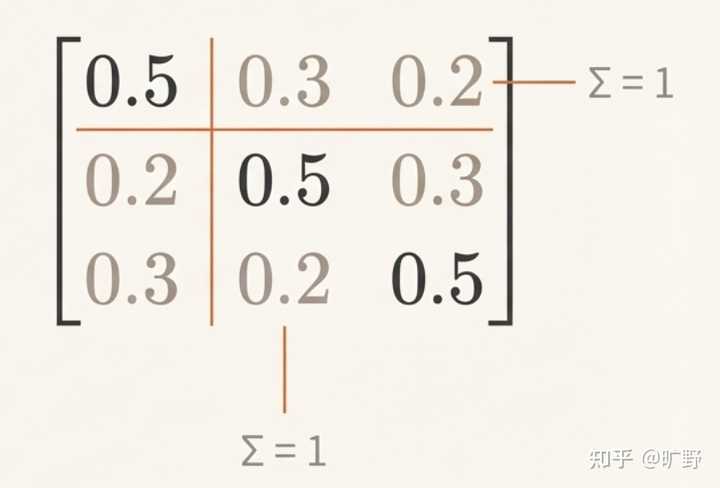
|
|
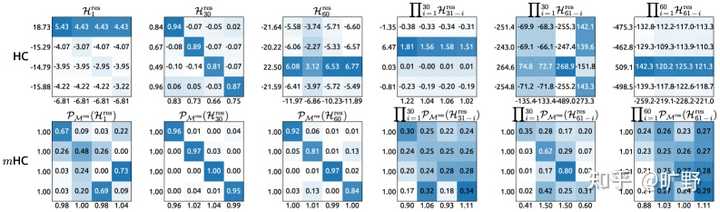
这个矩阵每一行相加都是 1,每一列相加也都是 1。这种矩阵有一种天然的”能量守恒”特性——它不会凭空放大或缩小信号。 而DeepSeek的这个选择,简直是神来之笔。 具体来看看双随机矩阵的一些性质,你就能明白Deepseek这样选择的深意。 先说谱范数的事儿。 双随机矩阵有个非常好的性质——它的谱范数,你可以理解为”最大放大倍数”,恒定小于等于 1。这个性质就是说不管你的信号怎么过这个矩阵,它最多保持原样,绝对不会被放大。还记得前面说的 HC 那个 3000 倍放大的灾难吗?双随机矩阵从根本上就杜绝了这种可能。 再说复合封闭性。 这个性质更妙——两个双随机矩阵乘起来,得到的还是双随机矩阵。这有点像说“龙生龙,凤生凤,老鼠的儿子会打洞”——不管你网络堆多少层,只要每一层的残差矩阵都是双随机的,那整个复合映射 \prod_{i} \mathcal{H}^{res}_i 依然保持双随机的性质。所以说稳定性不是靠运气,而是有数学上的铁保证。 最后还有关于它的几何意义。 这里要提一个概念叫 Birkhoff多面体。所有双随机矩阵构成的集合,在几何上形成了一个凸多面体,而这个多面体的顶点恰好就是所有的置换矩阵(0-1 矩阵,每行每列有且仅有一个 1)。也就是说任何一个双随机矩阵,都可以看作是若干个”纯粹的重新排列”的加权平均。 什么意思呢?如果ResNet的恒等映射像是”原封不动地传递信息”。那双随机矩阵做的事情,就像是在说:”我不只是原封不动,我允许把特征稍微重新洗一洗、混一混,但我保证这种混合是可控的、能量守恒的。” 这就形成了一种漂亮的泛化关系, 当残差流宽度 n=1 时,双随机约束退化成标量 1,也就是回到了最原始的恒等映射。mHC 并没有抛弃 ResNet,而是把它包进了一个更大的框架里。 这个约束选得太精妙了…… |
|
|
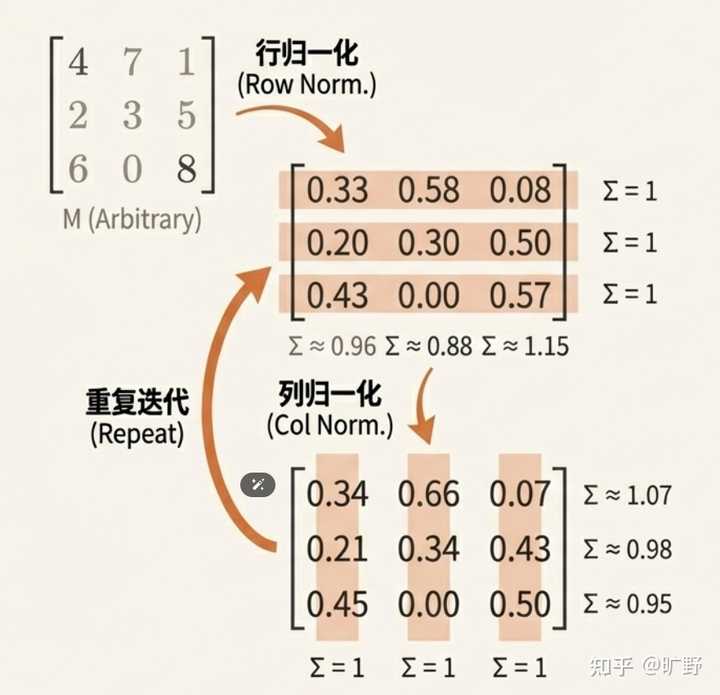
HC 与 mHC 的代表性单层/复合映射可视化;图中同时标注前向信号增益(行和)与反向梯度增益(列和)。mHC 的映射更接近“前后向增益≈1”的稳定传播目标Sinkhorn 迭代——优雅的投影算法 理论上的说完了,怎么保证训练过程中,矩阵始终落在双随机流形上? 这就涉及到一个经典的算法:Sinkhorn-Knopp 迭代。 算法的思路也很简单,有点像”打乒乓球”。比如你有一个普通的矩阵,想把它变成双随机矩阵,那就这么干: 先把每一行做归一化(让行和变成 1)再把每一列做归一化(让列和变成 1)但这时候行和又不是 1 了… 没关系,再归一化一次如此反复,来来回回地”打” |
|
|
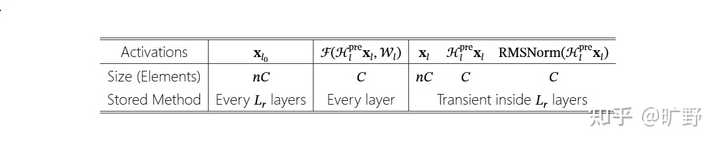
神奇的是,这个过程会收敛。理论上需要无穷多次迭代,但实践中 20 次左右就足够接近双随机矩阵了。写成公式的话: \mathbf{M}^{(t)} = \mathcal{T}_r(\mathcal{T}_c(\mathbf{M}^{(t-1)})) 其中 \mathcal{T}_r 是行归一化,\mathcal{T}_c 是列归一化。就这么简单。 但有个细节很重要,双随机矩阵要求所有元素非负,那原始矩阵如果有负数怎么办?DeepSeek 的做法是在迭代之前,先对矩阵元素取指数——e^x 永远是正数,问题解决。 这个算法有几个天然的好处,让它非常适合深度学习。它完全可微分,所以梯度能直接反传回去,不需要任何特殊处理;每次迭代就是矩阵运算,并行度极高,GPU跑起来好;收敛还很快,20 次迭代在现代硬件上几乎可以忽略不计。 DeepSeek 在工程实现上更进一步,他们把整个 Sinkhorn 迭代塞进一个 CUDA kernel 里,反向传播的时候不存中间结果,直接在 on-chip memory 里重算。这样既省了 HBM 带宽,又避免了显存占用。 但他们对于输入输出映射 \mathcal{H}^{pre} 和 \mathcal{H}^{post},mHC 没上双随机,只做了简单的非负约束(用 Sigmoid)。因为这俩是 1×n 的向量,根本不是方阵,没办法做”行列和都等于 1”的约束。用 Sigmoid 保证非负,已经足够防止正负系数互相抵消导致的信号衰减了。 该精细的地方精细,该简化的地方简化。这种取舍拿捏得恰到好处。 Deepseek的工程优化,6.7% 背后的硬实力 说完算法,就来到了工程层面。一个好想法如果没有高效的实现,就等于没有。 HC当初没能大规模推广,除了训练不稳定之外,还有一个问题就是太慢了。 传统的残差连接,每一层只需要读写 O? 个元素(C 是通道数)。但 HC 把残差流宽度扩展了 n 倍,I/O 成本直接涨到 O(nC)。问题是在GPU里计算往往不是瓶颈,内存带宽才是。这额外的 I/O 开销,在大规模训练中会像滚雪球一样放大。 那mHC是怎么解决这个问题的? 他们在Kernel Fusion上下了大功夫。把原本分散的多个小操作合并成一个大 kernel,这样数据只需要从 HBM 读一次、写一次,中间的所有计算都在 on-chip memory 里完成。他们用 TileLang 实现了混合精度的融合 kernel(bfloat16 计算 + float32 累加),还把 RMSNorm 里的除法挪到矩阵乘之后执行——数学上完全等价,但省了一次除法的内存往返。这种操作,真的能看出对硬件的绝对理解。 另一个核心优化是选择性重计算。这听起来有点反直觉:为什么要”重新算”?直接存下来不好吗? 问题在于存中间结果要占显存。在大规模训练中,显存往往是最紧张的资源——它直接决定了你能跑多大的 batch size。mHC那些小矩阵操作,像几十乘几十的矩阵乘法这种,算得飞快,重算的代价很低。但如果把这些中间结果都存下来,占用的显存却不少。 “空间换时间”还是”时间换空间”?mHC 选择了后者,用微量的重计算开销,换来更大的 batch 和更高的吞吐。 他们甚至推导出了最优的重计算块大小: L_r^* \approx \sqrt{\frac{nL}{n+2}} 这个公式就是在说应该把多少层打包成一个重计算单元,才能在时间和空间之间取得最优平衡。简洁,优雅,有理论支撑。 |
|
|
mHC 在连续 Lr层内的“激活存储 vs 反向重计算”划分,并据此推导峰值显存与最优重计算块大小 ? 最后是大规模分布式训练的适配。DeepSeek-V3 引入了一种叫DualPipe的流水线并行策略,而 mHC 需要和这套系统无缝协作。他们做了不少针对性优化:把关键的 \mathcal{F}_{post,res} kernel 放到专用的高优先级 CUDA stream 上,确保它能及时完成不拖后腿;Attention 部分特意不用 persistent kernel,这样当 mHC 操作需要 GPU 资源时可以随时抢占;重计算逻辑和流水线通信完全解耦,互不干扰。 |

|
|
mHC 的通信-计算重叠调度示意:在 DualPipe 基础上扩展以吸收 mHC 引入的额外开销,实现更高效的 pipeline stage 边界重叠 最终效果那就是惊人的n=4 的 mHC 只增加 6.7% 的训练时间开销。 |

|
|
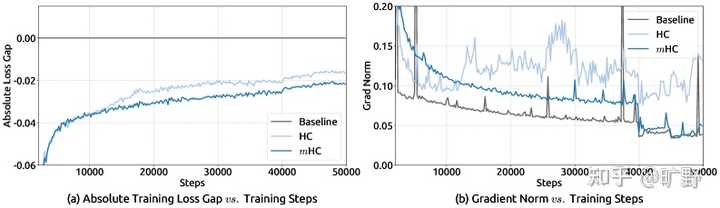
6.7%,考虑到 mHC 带来的性能提升和训练稳定性改善,这点代价简直可以忽略不计。如果有人告诉你,多花 6.7% 的训练时间,就能让你的 27B 模型在 BBH 上涨 7 个多点、在 GSM8K 上涨 7 个点,你干不干? 这笔账,怎么算都是血赚。 实验结果带来的全面碾压 27B 模型的实验结果,说实话有点夸张: |
|
|
27B 训练稳定性对比:mHC 与 baseline 的训练 loss gap 更优,同时梯度范数保持平稳;HC 则更易出现不稳定波动 |
|
|
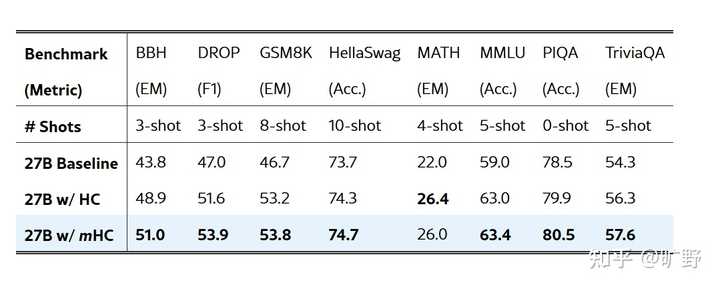
27B 模型在 8 个下游 benchmark 的 zero/few-shot 表现对比。mHC 在多数任务上优于 baseline,并在多项任务上超过 HC 8 个 benchmark,mHC 全面超越 baseline,在大多数任务上也超过了不稳定的 HC。 BBH 相对 baseline提升 7.2 个点,这个幅度在 27B 规模上已经非常可观了。要知道这只是通过改残差连接的拓扑结构实现的,没加参数、没加数据、没改训练流程。 更重要的是稳定性。mHC 的 loss 曲线平滑得像 baseline 一样,梯度范数也很稳定。而 HC 在 12k step 附近那个 loss spike... 在大规模训练中这种抖动是要人命的。Scaling实验也很漂亮。从 3B 到 9B 到 27B,mHC 相对 baseline 的优势始终保持。这说明这不是小模型上的 overfitting,而是真正的架构改进。 |
|
|
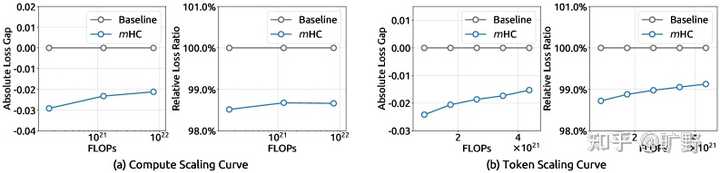
mHC 的 scaling 特性:在 compute scaling(不同算力预算的 compute-optimal 配置)与 token scaling(训练过程轨迹)上,相对 baseline 的优势保持一致最后的个人想法 跳出论文本身, 残差连接这个古董还有多少可挖的空间? 在 mHC 之前,我一直觉得残差连接已经是个"已解决"的问题了。He Kaiming那篇Identity Mappings in Deep Residual Networks 把道理讲得透透的,后人只需要照抄就完事。 但 mHC又告诉我们,即使是看似最基础、最"完美"的设计,也存在泛化的空间。关键是要找到正确的约束——既能拓展表达能力,又能保持原有的好性质。 双随机矩阵这个选择,就是在"自由度"和"稳定性"之间找到了一个甜点。属于一种四两拨千斤的操作,很厉害。 DeepSeek 的工程能力也是越来越恐怖了。 从 V2 的 MLA 到 V3 的 DualPipe,再到现在 mHC 的 kernel 优化,DeepSeek 展现出来的系统工程能力是国内甚至国际顶尖的。算法创新当然重要,但把算法创新高效落地的能力同样关键。很多学术界的好想法最后没能普及,往往就是因为 overhead 太大。mHC 把额外开销控制在 6.7%,这是真正的工程功底。 现在的AI不是"有个好 idea 就能发顶会"的时代了。 你得能训、能量化、能部署。不然你的创新就只能躺在论文里积灰。DeepSeek 这帮人显然深谙此道。 还有就是Macro Design可能是下一个金矿。 这几年大家都在卷Attention变种(MQA、GQA、MLA)和 FFN 结构(MoE、GLU)。这些属于 Micro Design——相当于在打磨每一块砖的质地。 但 Macro Design——也就是层与层之间怎么连接、信息怎么流动——相对被忽视了。这相当于建筑的框架结构。可也许我们一直在用最先进的砖,盖着最传统的房子。DenseNet 当年提出 dense connection,但因为内存开销太大被放弃了。现在硬件变强了,工程技术也进步了,也许是时候重新审视这个方向了。 那些理所当然的默认选项,可能往往就是最大的突破口。 残差连接如此,LayerNorm 如此,Softmax 可能也是如此。 DeepSeek 这帮人是真卷啊。残差连接都被他们玩出花来了,下一个是啥?LayerNorm?Softmax? 我拭目以待。 如果觉得文章对你有帮助,欢迎点赞关注一波~ 我是旷野,带你探索无尽技术! 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
打那么多字干嘛,你们写着不累,我看着都累,就简单说说吧。 首先说一下,这篇论文跟黎曼流形优化没关系,跟最优传输也没关系,没太多数学,放心看。 我们先从 ResNet 的残差开始说起,之前的结构是 \mathbf{x}_{l+1}=\mathbf{x}_l+\mathbf{f}(\mathbf{x}_l) ,这里给了一个 shortcut,直接将 \mathbf{x} 传到下一层。 但是呢,这是单流结构,也就是只有一个 \mathbf{x},信息通道的带宽太窄,在大网络中就变成了瓶颈。 字节写了篇论文 HC,就是把单流变成 M 条流,之前的向量变成了矩阵: \mathbf{X}_{l+1}=\mathbf{H}_{res}^l \mathbf{X}_l+\mathbf{H}_{post}^lF(\mathbf{H}_{pre}^l \mathbf{X}_l) 但是问题也来了,当我们忽略残差时,第 L 层大约为 $$ \mathbf{X}_L\approx\left(\prod_{l=1}^L\mathbf{H}_{res}^l\right)\mathbf{X}_0 $$ 如果 H 的谱范数,也就是最大特征值不恒为 1,那么在多层累乘下,最终的 X 的谱范数会变得非常大或非常小,也就是梯度爆炸或梯度消失,导致训练不稳定。 所以正常人都会想到把 H 的谱范数设定为 1,这里就有很多种选择: 谱归一化,就是简单粗暴地除以最大奇异值,但这会导致某一条流极强,其他流被压制,看起来就不利于传输信息的样子正交化,做一个 SVD,然后把奇异值都变成 1,这个看起来好像没问题, 而且你也可以宣称是Stiefel 流形,也是很唬人利于包装的名字,但缺点是很多 AI 小将可能不知道怎么写 SVD,而且 Householder 变换也慢,还是算了双随机矩阵,用Sinkhorn 算法把原矩阵投影到双随机矩阵空间。这个好啊, Sinkhorn 就是矩阵乘法,迭代几次也收敛得快,那就是它了。 所谓投影,就是在双随机多面体中,寻找原矩阵KL散度最接近的矩阵。 所谓Sinkhorn 算法,就是一个交替投影算法,在行约束流形和列约束流形之间交替进行 KL 投影,最终收敛到它们的交集,也就是双随机流形上。 但最后写论文了,如果说我的贡献就是把一个矩阵行归一化再列归一化,那肯定不好看,那就包装一下: 双随机矩阵不fancy,改成Birkhoff Polytope谱范数约束不fancy,改成流形约束交替投影算法不fancy,改成Sinkhorn 算法 这下终于 fancy 了,意满离。 最后叠甲,论文是好论文,包装也是学术圈惯例,但别过度神话 DS,正常讨论就好。 |
|
字节的HC超连接,占有六到七成贡献,提出了新的技术范式。 DeepSeek的mHC流形约束超连接,占有三到四成贡献,大大提升了大模型上的可用性,补齐了稳定性和经济性。 大概可以理解为:字节豆包搞出来一个核聚变方案,DeepSeek给他套了一个托卡马克环。(mHC这个词看起来就像核工业里面的名词。笑) 字节的HC,是一种高爆美学,初衷为了解决预/后层归一化问题(这是残差连接的一个顽疾,在炸膛和钝化中做选择)。 残差连接(无论是 Pre-Norm 还是 Post-Norm)都有一个共同的局限:它们预先定义了层输入与输出之间的连接强度,而不是让神经网络自主学习最优的连接比例。 字节提出了全新的“物种”,在所有人都还在传统的 Residual Connection里打转时,字节跳动第一个跳出来说:要搞加法?为什么不能是矩阵乘法? 这是HC的一个爽点。 ?证明了“可行性”,字节不仅提出了想法,还在 1B 和 7B 这种中小规模的模型上跑通了,证明了这种疯狂的架构不仅能跑,而且收敛速度还能快 1.8 倍。 但由于缺乏约束,它会“开锅炸膛”,最大的坑是显存带宽,HC连接矩阵自由生长,导致信号在多层堆叠后出现“指数级爆炸”。 ?字节虽然在 7B 模型上跑通了,但 DeepSeek 在跑 27B 甚至更大模型时发现,原始的 HC 跑到 1.2万 步左右就会“开锅”(Loss 突然飞升,梯度乱跳)。 这车好是好车,就是开久了会掉坑里,还会滋滋冒烟。(在27B模型下, 原始 HC 由于缺乏约束,其复合映射的增益强度峰值达到了3000) ?DeepSeek 指出 HC 的核心问题是破坏了“残差连接的恒等映射”,于是引入 Sinkhorn 投影算法把矩阵框死在“双随机流形”里,这就是m流形,这个词的来源。 HC 虽然参数少,但特别吃显存带宽。DeepSeek 为了能让这个技术在超大模型上用得起,搞了 Kernel Fusion 和 DualPipe。 从残差连接(加法)→字节HC(无约束的矩阵乘法)→DeepSeek mHC (流形约束的矩阵乘法) 这是一个经典→跳跃→优化的一个历史流变。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
大过节的qwen发布了image 2512,DeepSeek这边就偷摸的在arXiv 上挂出了这篇 mHC: Manifold-Constrained Hyper-Connections (arXiv:2512.24880),哪个正经公司在最后一天还发论文啊。 简单的看了一下,说说我的看法: 这回DeepSeek又要对 残差连接(Residual Connection)出手了。 现在我们模型的底层架构就是叠 Transformer Block,而过去这十年,对于每一层的堆叠,恺明大神的 ResNet 也就是那个 y=x+f(x),几乎行业的“公理”。它通过 Identity Mapping(恒等映射),可以让信号能无损传下去,梯度也能无损传上来,这就保证了咱们能把模型堆到几百上千层还不崩。 但 DeepSeek 团队之前(大概是去年 9 月那会儿)提了个 Hyper-Connections (好像看的人不多,我当时没太注意这个) 的概念,觉得简单的相加太浪费了就搞了个更复杂的连接方式来扩宽层间的信息通路。但是一旦你动了那个“相加”,Identity 的属性就没了,梯度传播就开始不稳定,这样训练起来特别容易炸他们管这叫 Seesaw Effect(跷跷板效应)。 这篇 mHC 就是来填这个坑的,咱们顺着逻辑拆解一下。 |
|
|
这就引出了 mHC 的核心:流形约束(Manifold Constraint)。 别被这数学名词吓着:之前的 HC 是想让连接权重随便长,结果就长歪了;现在的 mHC 就是给这些权重矩阵加了个限制。DeepSeek 在数学上证明了,如果把这些超连接的权重矩阵强制投影到一个特定的流形空间里就能在保留 HC 那种高带宽、多通路优势的同时,还把 Identity Mapping 的属性给找补回来。 也就是说他们在数学层面上造了一个“既要有又要”的结构:既要连接方式足够复杂多变,能捕捉更高级的特征交互;又要信号传播像 ResNet 一样顺滑,不至于在深层网络里迷路。 这里的“流形”具体由两个关键的数学性质构成: 第一是 谱范数约束(Spectral Norm Constraint),他们强制要求连接矩阵的谱范数 ∥W∥2≤1。这在动力系统里叫“非扩张”(Non-expansive)。只有当矩阵的最大奇异值被摁在 1 附近,信号能量在深层传播时才不会发散。 第二是 双重随机矩阵(Doubly Stochastic Matrices), 这是一类行和、列和都为 1 的非负矩阵。这玩意儿有个极好的代数性质叫 闭包性(Compositional Closure)。两个双重随机矩阵乘起来它还是双重随机的,所以这就保证了无论网络堆多深,整体的变换性质不变。更重要的是,这让每一层的输出变成了上一层的 凸组合(Convex Combination),从根本上恢复了训练的稳定性。 并且论文里面包含了很强的理论推导,对于信号传播(Signal Propagation)的分析非常扎实,直接指出了为什么之前的架构在超深层会遇到瓶颈,而 mHC 是怎么通过约束奇异值分布来解决这个问题的。(ps:DeepSeek 的日子也是好起来了,做实验都敢用27B的模型了,HC那篇用的可以是7B的) |
|
|
论文里还有一段非常精彩的理论分析,是从 动态系统(Dynamical Systems) 的角度去看的。 如果你把层数看作时间步,深层网络其实就是一个离散的动态系统。而且这篇论文证明了在流形约束下,这个系统的 Lyapunov 指数是受控的。他们通过一种类似 Projecting(投影)的手法,确保权重矩阵始终保持良好的 谱性质(Spectral Properties)。说的通俗点就是:不管怎么更新,这些矩阵在数学性质上必须看起来像一个“稍微扭曲了一点点的 Identity Matrix”,而不是一个完全随机的矩阵。 这就从理论上解释了为什么 mHC 可以堆叠到成百上千层而不崩塌,这部分其实是对现有架构理论的一个重要补充。以前我们只知道“加个残差就好使”,现在 mHC 告诉我们:“只要你在流形上走路,哪怕姿势复杂点,也不会摔倒”。 而且熟悉 DeepSeek 风格的朋友都知道,他们从来不只聊数学,还必须要聊 System Efficiency。 mHC 这个架构显然是做过严格的 Infrastructure Optimization 的。如果只是理论上好使但拖慢了训练速度,DeepSeek 是绝对不会用的。他们在论文里也提到了这点,这种特殊的连接方式配合专门优化的 CUDA kernel,可以把额外的计算开销压缩到了几乎可以忽略不计的程度。 这就很可怕了,等于是在算力成本几乎不变的情况下,白嫖了模型表达能力的上限。在实际的大规模训练吞吐上并没有造成明显的 overhead。 这对咱们行业意味着什么? 我觉得这可能是“后 Transformer 时代”的一个重要信号。以前咱们扩模型,就是简单粗暴地增加层数、增加宽度,属于“堆料”。但 mHC 提示了一个新的方向:层与层之间的拓扑结构(Topology)本身,还有巨大的挖掘空间。 如果这种基于流形约束的连接方式被验证能 scaling up 到万亿参数级别(论文说 671B 的 MoE 模型是ok的),那咱们以后设计大模型,可能就不再是简单的搭积木而是要开始研究积木之间的粘合剂怎么调配了。 mHC 的出现不仅修复了 Hyper-Connections 的缺陷,更重要的是它将深度学习架构设计的视角从单纯的“连接图”提升到了“参数流形”的高度。随着基础模型对效率和能力的要求日益严苛,mHC 所代表的几何约束设计理念,极有可能成为未来几年 AI 基础设施的核心标准之一。 26.1.2 更误 Hyper-Connections 是我记错了,我刚又检查确认了一下是自字节的论文,是我这边搞混了。 然后Dynamical Systems应该翻译成动力系统,我也再次更正下 最后感谢各位提醒 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
|
| [收藏本文] 【下载本文】 |
| 科技 最新文章 |
| 为什么有些人不敢使用微信? |
| 作业帮 iOS 版应用被曝存在假卸载按钮设计, |
| 你认为稀土是中国手里的终极王牌吗? |
| 如何看soul这个软件? |
| 如何看待FARS批量制造100篇论文? |
| 为什么有些用户宁愿看盗版,也不愿为正版视 |
| 英政府拟强制中资桥接芯片巨头FTDI出售80%股 |
| 如何看待姚班大神陈立杰官宣入职 OpenAI? |
| 微信有多傻逼? |
| 如何看待「斩杀线」概念的出现及其影响? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |