| |
|
| 知识库 -> 工程技术知识 -> 为什么几乎所有教科书上对微分的讲解都不明不白? -> 正文阅读 |
|
|
[工程技术知识]为什么几乎所有教科书上对微分的讲解都不明不白? |
| [收藏本文] 【下载本文】 |
|
比如:d 的定义(运算符?标记?),dy 与 dx 的定义(未知数?文字?),高阶微分 d?y 的定义、运算法则、定理、推论、性质、应用。 定义→性质… |
|
好问题。 这个问题问到点子上了,绝对是国内数学教育里一个祖传的「坎」。 你觉得教科书讲不明白,根子不在你,在于国内大部分《高等数学》或《微积分》教材,在「微分」这个概念上,试图把两种完全不同,甚至在历史上是互相对立的体系,强行缝合在一起,又不愿意花篇幅讲清楚它们的来龙去脉。 哪两种体系? 历史的、直观的、物理学家的「无穷小量」体系。现代的、严谨的、数学家的「线性逼近」体系。 咱们国内的教科书,往往是用着第二种体系的严谨化定义(比如极限),但讲解和符号系统里,却大量残留着第一种体系的直观「感觉」。这就好比你拿到一个用现代分子料理技术做出来的汉堡,但说明书却用古代炼丹术的术语来写,什么「取太阳精粹之肉饼,辅以太阴凝露之酱汁」,能不懵吗? 下面我用大白话给你讲一下。 d,dy,dx到底是个啥玩意儿? 我们必须在现代数学分析(也就是「线性逼近」体系)的框架下讨论这个问题,不然就又回到了三百年前的玄学争论里。 1. 先说 dx 是什么。 忘掉「无穷小增量」这个概念。在函数 y = f(x) 的微分里,dx 就是一个自变量,一个普通的实数,跟 x 本身没半毛钱关系。 你可以把它当成 h,可以当成 Δx,它叫什么都行,它就是一个用来衡量变化的「尺子」。它的取值范围是整个实数域 R。对,你没看错,dx 可以等于1,可以等于-100,也可以等于π。它不是一个趋近于0的量。 2. 再说 dy 是什么。 dy 也不是「y的无穷小增量」。dy 是一个因变量,它的值依赖于 x 和 dx。dy 的定义是: dy = f'(x) * dx 看清楚,这是一个定义式。f'(x) 是函数 f 在点 x 的导数,这是一个确定的数。所以,dy 本质上是一个关于 x 和 dx 的二元函数。更准确地说,在固定一个点 x? 之后,dy 是一个关于 dx 的线性函数。它的图像是一条过原点的直线,斜率是 f'(x?)。 3. 最后说 d 是什么。 d 是一个运算符,叫微分算子。它作用在一个函数 f 上,会得到一个新的东西,叫 df。这个 df 是什么呢?它是一个函数,这个函数在每个点 x 的值,是那个点上的线性映射。 听着有点晕?我换个说法: d 作用在 f 上,得到 df。 df 在点 x 的值,记作 df(x) 或者 d_x f,它本身是一个线性函数,这个线性函数的功能是:你给它一个输入 dx,它就输出 f'(x)dx。 所以 dy = df(x)(dx) = f'(x)dx。 这个视角下,d/dx 这个符号就很好理解了,它就是把 df 这个函数除以 dx 这个函数(这里dx是恒等函数g(x)=x的微分,g'(x)=1,所以dx = 1*dx)。这个说法不完全严谨,但是能帮你直观理解。 总结一下严谨的定义: dx:自变量的增量,一个独立的实数变量。dy:函数增量 Δy = f(x+dx) - f(x) 的线性主部。当dx很小时,Δy ≈ dy。微分 dy 是对非线性的增量 Δy 的一个线性近似。这是微分的灵魂。d:微分算子,它把一个函数映射到它的微分(一个线性映射场)。 你提到的多元函数中 d 是个标记,后面又变成运算符。没错,这正是概念混淆的重灾区。在多元函数 z = f(x, y) 中,dz = (?f/?x)dx + (?f/?y)dy。这里的 dx 和 dy 同样是独立的实数变量,分别代表在x方向和y方向的增量。dz 依然是全增量 Δz 的线性主部。这里的 d 依然是那个微分算子,只不过它作用在了多元函数上。 为什么教科书不这么清清楚楚地讲? 因为历史包袱太重了。 莱布尼茨当年引入 dy/dx 这套符号的时候,他脑子里想的就是无穷小量的比值。这套符号系统在计算上太强大、太符合直觉了,以至于物理、工程领域的人用了几百年,爽得飞起。比如链式法则 dy/dx = (dy/du) * (du/dx),写成分数形式,就像可以约分一样,多直观! 后来柯西和魏尔斯特拉斯等人为了解决数学危机,用 ε-δ 语言建立了严格的极限理论,把无穷小量这个「幽灵」从数学分析里驱逐了出去。微分被重新定义为我们上面说的「线性逼近」。 但问题来了,dy/dx 这套符号已经深入人心,完全抛弃是不可能的。所以教科书就陷入了一个尴尬的境地: 它想告诉你微分的本质是线性逼近(所以会有 Δy = AΔx + o(Δx) 这样的定义),但又想保留莱布尼茨符号的计算便利性。 于是,它就在讲解 dy, dx 的时候,含含糊糊地说是「微小的增量」,让你往无穷小上靠拢,方便你直观理解和计算。但考试证明题的时候,又要求你用 ε-δ 或者线性逼近的定义,不承认无穷小。 这种教学上的「精神分裂」,导致了你的困惑。 在我们算法工程师眼里,微分意味着什么? 这个「线性逼近」的思想,在我的工作中几乎无处不在。我给你举个实际的例子。 场景:优化一个深度学习模型。 一个神经网络,不管多复杂,本质上就是一个巨复杂的复合函数 Loss = F(W),其中 W 是模型里成千上万甚至上亿的参数(权重)。我们的目标是找到一组 W,让 Loss 最小。 怎么找?用梯度下降法。也就是每次把 W朝着能让 Loss 下降最快的方向挪一小步。这个「最快的方向」,就是梯度的反方向,-?F(W)。 梯度是什么?梯度就是由所有偏导数 ?F/?W_i 组成的向量。而每个偏导数,本质上就是微分思想的体现。 当我们计算梯度时,我们实际上在做一件事情:在当前的参数点 W 附近,用一个**线性函数(一个超平面)**去近似 Loss 这个复杂的非线性函数。这个线性函数的斜率信息,就由梯度向量 ?F(W) 决定。 ΔLoss ≈ ?F(W) ? ΔW 这个公式,是不是和 dy ≈ f'(x)dx 长得一模一样?只不过是高维版本。 dy 对应 ΔLoss,f'(x) 对应梯度 ?F(W),dx 对应参数的微小变化 ΔW。 我们相信,只要 ΔW 足够小,这个线性近似就是可靠的。所以我们沿着 -?F(W) 方向走一小步,就能保证 Loss 基本上是下降的。然后我们到了新的 W' 点,再在这个新点做一次线性近似,再走一小步…… 这就是梯度下降的本质。 整个现代AI的基石——反向传播算法(Backpropagation),说白了就是应用链式法则高效计算这个巨复杂函数的梯度。它每一步计算的,都是函数在某个局部通过微分建立的线性关系。 如果脑子里想的是「无穷小」,那你很难理解为什么我们能用有限大小的「学习率」去乘以梯度来更新参数。但如果你理解了微分是「线性逼近」,一切就顺理成章了:我们就是在用一个局部最好的线性模型,来指导我们在非线性的复杂山谷里,一步步走到谷底。 关于高阶微分 d?y 你问的这个问题非常深刻。d?y 是一个更大的坑。 对于一阶微分 dy,它有明确的几何意义:切线(或切平面)上的增量。 但是二阶微分 d2y 呢?d2y = d(dy) = d(f'(x)dx)。根据乘法法则,这玩意儿展开会变成 d(f'(x))dx + f'(x)d(dx) = f''(x)dx2 + f'(x)d2x。 在大多数初等微积分里,为了让 d2y/dx2 = f''(x) 这个好看的等式成立,会强行规定 x 是自变量时,d2x = 0。这是一个非常粗暴且不讲道理的规定,纯粹是为了形式上的方便。 在更现代的微分几何语境下,高阶微分会涉及到更复杂的结构,比如「射流丛」(Jet bundle),远远超出了初等微积分的范畴。 所以,给你的实用建议是: 在学习《高等数学》这个阶段,不要去深究 d2y 或 d?y 本身的独立含义。就把 d?y/dx? 看作一个不可分割的整体符号,它就等于 f 的 n 阶导数 f???(x)。这能帮你绕开绝大多数的认知障碍。等你以后学习微分流形之类的课程,再回过头来重新审视它。 如果你真的想把这个根子上的问题彻底搞懂,我推荐你跳出国内教材的思维定式,去看一些好的资源。下载地址:推荐几本冷门但是含金量极高的微积分读本(附PDF下载),我再来详细介绍下: 打好基础,看思想源头: 《Calculus》 by Michael Spivak: 这本书是数学系本科一年级的经典分析入门教材。它从最基本的ε-δ语言出发,非常严谨地构建了整个微积分体系。关于微分,它会让你彻底明白什么是「线性逼近」。看完这本书,你对微分的理解会上升一个层次。 |

|
|
《普林斯顿微积分读本》:如果觉得Spivak太难,这本书是一个非常好的过渡。它讲得非常直观,同时又不失严谨,会把很多概念背后的思想给你讲透。 换个视角,看现代观点: 《微积分的历程:从牛顿到勒贝格》:这本书能帮你理清微积分发展的历史脉络,让你明白为什么会有「无穷小」和「极限」两种体系的斗争和演变。理解了历史,很多困惑就迎刃而解了。 |

|
|
如果未来有兴趣,可以看看微分流形的入门书籍,比如 《Introduction to Smooth Manifolds》 by John M. Lee。在这里,d 会被正式定义为外微分算子,你会看到一个无比和谐与强大的数学体系,之前所有的困惑都会烟消云散。 |

|
|
作为一名在数学之路上探索踩坑了很久的人,深知优质教材对于数学学习非常重要。因此,精心搜集了76本国外经典数学教材,涵盖代数、几何、分析、概率等多个数学分支,希望能帮助热爱数学的同学们构建更完善的知识体系。 76本国外经典教材,全方位覆盖代数、几何、分析、概率等核心领域(附PDF下载) 此外,见证国内数学学科发展的“活化石”,科学出版社的《现代数学基础丛书》自1981年诞生以来,已持续更新至204卷,堪称中国数学界的“四库全书”,也一并整理好了。 5000字硬核盘点!《现代数学基础丛书》204卷必读清单(附PDF及领域分类),建议收藏备用 ! 你觉得教科书讲得不明不白,这恰恰说明你的数学品味很好,你在追求一种逻辑上的和谐与自洽。这不是钻牛角尖,这是学好数学(以及任何硬核科学)最宝贵的品质。 不要把 dy, dx 当作某种神秘的、需要「意会」的东西。在现代数学里,每一个符号都有它精确的、冰冷的定义。只不过我们现在的入门教材,为了所谓的「降低难度」,把这些定义背后的道理给阉割了,给你留下了一堆看似直观却充满矛盾的「规矩」。 忘掉无穷小,拥抱线性逼近。这是你捅破这层窗户纸的关键。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
之前写过不少关于微分和导数的文章: 微分是什么?dx,dy是什么?微分和导数的关系是什么?\cdots\cdots 今天这篇文章再换一个角度来谈论微分和导数,让我们从微分出现的原因说起。 1 微分出现的原因 出于种种原因,我们可能想去求曲线的长度、曲面梯形的面积: |
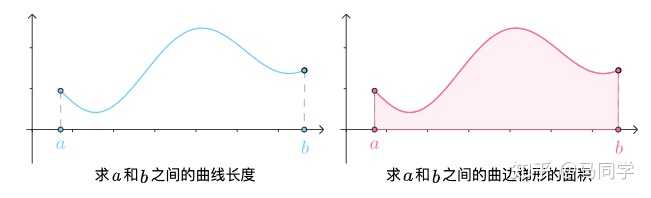
|
|
求解思路是这样的,以求曲线长度为例,将曲线分为多个部分,每一部分都用切线来近似曲线: |
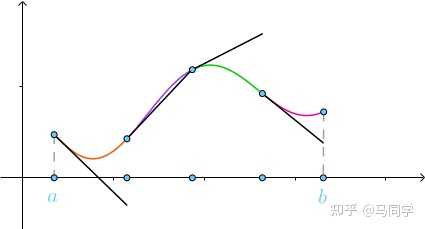
|
|
划分的越细,直到划分为无穷多份,最终这些切线的长度加起来就是曲线的长度: |
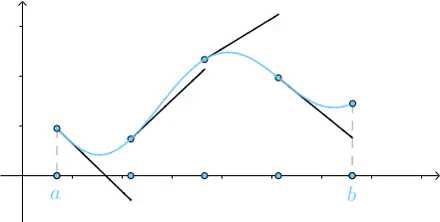
|
|
求曲边梯形面积也是类似的,用小矩形来近似曲边梯形的面积,随着小矩形的增多最终得到曲边梯形的面积: |
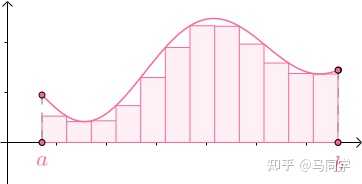
|
|
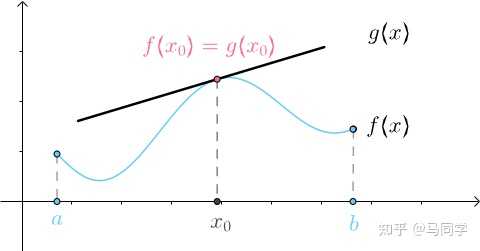
上面的思想就是微积分的核心思想,“以直代曲”。曲线长度、曲边梯形就是“曲”,切线、小矩形就是用来近似(代替)的“直”,这种“直”就是 微分。关于这里还不了解的可以看“微分是什么?”这篇文章。 2 微分与导数 先不谈曲边梯形,本节先来回答曲线的微分是什么,也就是可以近似曲线的直线是什么? 2.1 几何分析 下面结合几何来理清一下求解的思路。假设有曲线f(x) 和直线g(x) ,如果两者完全相等,那么有: f(x)=g(x)\quad 或\quad f(x)-g(x)=0\\ 很显然这在整个曲线和直线上是做不到的,但肯定可以做到在某点上相等,比如让它们在x_0 点相等,从几何上看就是曲线f(x) 和直线g(x) 在x_0 点相交: |
|
|
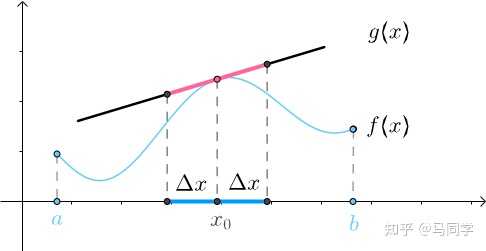
下面要更进一步,不过不要太贪心,只希望两者在x_0 附近尽量相等。比如像下图一样,在(x_0-\Delta x,x_0+\Delta x) 的区间内,曲线f(x) 和直线g(x) 相差很小: |
|
|
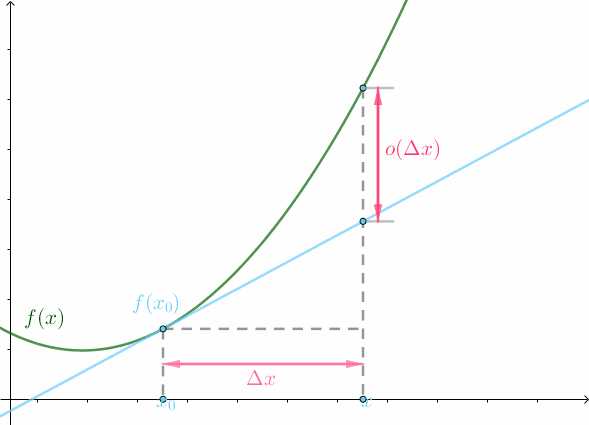
这点如果可以做到,那就可以按照上一节说的,将曲线分成n份,每份都用各自的微分来近似。 2.2 代数分析 通过几何分析,思路已经理清楚了,要找的微分(直线)需要满足以下两点: (1)曲线f(x) 和直线g(x) 要交于x_0 点。假设直线g(x) 的斜率为k ,那么根据点斜式,可得直线函数: g(x)=f(x_0)+k(x-x_0)\\ 这里面就是k 还未知,求出了k 就得到了想要的直线,也就得到了微分。 (2)曲线f(x) 和直线g(x) 要在(x_0-\Delta x,x_0+\Delta x) 的区间内尽可能相等。用代数表示即为: f(x)-g(x)\approx 0,\quad x\in(x_0-\Delta x,x_0+\Delta x)\\ 有约等号的式子是没法计算的,引入高阶无穷小o(\Delta x) 可以将约等号去掉: f(x)-g(x)=o(\Delta x),\quad x\in(x_0-\Delta x,x_0+\Delta x)\\ 高阶无穷小o(\Delta x) 的意思就是在\Delta x 这个范围内无限的接近于 0。至于为什么它无限接近于 0,以及为什么是高阶无穷小,在文章的最后会进行补充说明。 2.3 解出直线的斜率k 经过上面的分析我们有了: \left.\begin{aligned} g(x)=f(x_0)+k(x-x_0)\\ f(x)-g(x)=o(\Delta x) \end{aligned}\right\}\implies f(x)-f(x_0)-k(x-x_0)=o(\Delta x) \\ 这已经足够让我们解出直线的斜率k 了。注意到\Delta x=x-x_0 ,可以进行如下变形: \begin{aligned} f(x)-f(x_0)-k(x-x_0)=o(\Delta x) &\implies f(x)-f(x_0)-k\Delta x=o(\Delta x)\\ &\implies \frac{f(x)-f(x_0)-k\Delta x}{\Delta x}=\frac{o(\Delta x)}{\Delta x} \end{aligned} \\ 两侧取极限可得: \lim_{\Delta x\to 0}\frac{f(x)-f(x_0)-k\Delta x}{\Delta x}=\lim_{\Delta x\to 0}\frac{o(\Delta x)}{\Delta x}\implies \lim_{\Delta x\to 0}\frac{f(x)-f(x_0)-k\Delta x}{\Delta x}=0 \\ 略微作一下化简可得: k=\lim_{\Delta x\to 0}\frac{f(x)-f(x_0)}{\Delta x}\\ 至此我们就求出了k ,也就找到了f(x) 的 微分(直线g(x)的形式还需要变一下才是真正的微分,关于这点可以参考“dx,dy是什么?”这篇文章)。 这个k 在微积分中又有一个专门的名字,称为f(x) 的 导数。k如果存在(因为k是通过极限求得的,这个极限有不存在的可能),那么就称f(x)可导。 上面的思路还可以进一步思考,如果要找最接近曲线f(x) 的多项式曲线呢?这会得到泰勒公式,就留给大家作课后习题吧。 3 补充说明 这里补充说明两点: (1)高阶无穷小o(\Delta x) 为什么表示在(x_0-\Delta x,x_0+\Delta x) 的区间内无限接近于 0 ?这是因为它满足: \lim_{\Delta x\to0}o(\Delta x)=0\\ 上面这个极限式意味着\Delta x 越小,也就是越接近于x_0 点,o(\Delta x) 越接近于 0。用动画表示就是: |
|
|
上图中绿线就是曲线f(x) ,蓝线为微分,可以看到随着\Delta x 缩小,两者之间的距离o(\Delta x) 也无限接近于 0。 (2)为什么一定要高阶无穷小?同阶无穷小行不行?关于这点可以参考“为什么算出来的圆周率 π 等于 4 ?”这篇文章。 更多内容推荐马同学图解数学系列 |

|
|
广告 《马同学图解微积分(上)》数学图书TOP1 京东 ¥69.50 去购买? |

|
|
广告 马同学图解线性代数(数形结合,形象生动) 京东 ¥128.00 去购买? 送礼物 |

|
|
[img_log] [img_log] 4 人已送礼物 |
|
我正准备好好讲讲微分,就有人问这个问题了。表面上是教材讲不清楚微分,实际上是教材讲不清楚函数。我一再强调这一点,希望读者明白,这不是因为矫情。 考虑这样一个问题:设 y=2x, 求函数 \sin y 的最小正周期。 你认为答案应该是 2\pi 吗?恐怕你更有可能认为答案是 \pi, 因为 \sin y=\sin 2x, 然后认为自变量应该是 x. 这就是表述不明确的简单例子,提醒你关注函数到底是变化的数还是数的变化。 另一方面,如果现在规定函数 f\left(x\right)=\sin 2x, 即明确了函数是 f, 那么 x 在其中只是个辅助。意思是说,改称 f\left(y\right)=\sin 2y, 完全没有改变含义。这说明函数是数的变化。 今天我们只谈一元微积分中的微分。首先从一个简单的应用开始。 设 n\in\mathbb N^*, 则当正数 a 充分小时 \left(1+a\right)^n\approx 1+na, 这是为什么?设函数 f\left(a\right)=\left(1+a\right)^n, 则由二项式定理得到 f\left(a\right)=\sum_{k=0}^n\mathrm C_n^ka^k. 当 a\to 0 时, a^k 1\right)">\left(k>1\right) 是 a 的高阶无穷小量,因此在近似计算时可以忽略。 你是否想过,如果导数真的是微分学中的本质,那么为何不把微分学称为导数学呢?如果认为微分是微分学的本质,那么必然要把微分的基本思想讲清楚。 在实际应用时会遇到很多复杂的函数,我们甚至很难找到它们的表达式,但是它们往往在一个很小的范围内可以用一类很简单的函数近似。例如在刚才的例子中,就把函数 f 在 0 附近近似为 \hat f\left(a\right)=1+na. 这就是微分的基本思想。 设函数 f 在 x 的某一邻域上有定义,且存在线性函数 l 使得 f\left(x+\Delta x\right)=f\left(x\right)+l\left(\Delta x\right)+o\left(\Delta x\right)\quad\left(\Delta x\to 0\right), 则称 f 在 x 处可微。 什么是线性函数呢?其实就是形如 l\left(x\right)=kx 的函数,也称为正比例函数。 在这个概念中,就会体现出准确理解函数概念的重要性。教材不重视函数概念,就容易引导人把线性函数理解为 kx 或者 k, 然后理解不了微分概念。 再来解释微分当中的 \mathrm d. 教材往往很喜欢说 \mathrm df\left(x\right)=f'\left(x\right)\mathrm dx, 却不明确告诉你 \mathrm d 是什么东西。其实 \mathrm dx 就是一个虚拟的无穷小量,同时表示在近似计算时,可以忽略其高阶无穷小量。 当我们说 \mathrm dy=k\mathrm dx 时,就是说当 x 做一个微小的变化时, y 产生了近似于 k 倍的变化。因此当 f 在 x 处可微时,可以记 \mathrm df\left(x\right)=l\left(\mathrm dx\right). 注意到 f 和 f\left(x\right) 不是一回事,也就不应该把 \mathrm df\left(x\right) 写成 \mathrm df. 另外, \mathrm dy=k\mathrm dx 也可以理解为当 y 做一个微小的变化时, x 产生了近似于 1/k 倍的变化(如果 k\ne 0 )。因此,不必关心到底 x,y 谁是自变量,谁是因变量。 微分是本质,导数是求微分的具体方法。为了确定到底将函数在局部用哪个线性函数近似,我们找到了一种系统方法是求导数。设函数 f 在 x 的某一邻域上有定义,且 \lim_{\Delta x\to 0}\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}=k\in\mathbb R, 则称 f 在 x 处可导,称 k 为 f 在 x 处的导数,记为 f'\left(x\right). 不难证明, f 在 x 处可微的充要条件是 f 在 x 处可导,并且导数和微分直接相关。结合这两方面,就可以理解教材中的 \mathrm df\left(x\right)=f'\left(x\right)\mathrm dx 是什么意思了。 有些教材看起来并不是作者没有理解这些东西,而是没有讲清楚。也有些教材可能是作者根本就不理解,所以讲不清楚。但不论是哪种情况都不太好。我并不认为在基础教材中讲得不严谨会对学生有任何好处,难的东西可以不讲,但不能讲得不透彻,否则只会起到反作用。 送礼物 [img_log] [img_log] |

|
|
3 人已送礼物 |
|
这个问题问到了点子上,甚至可以说,这个问题触碰到了高等数学教育中一个几十年来心照不宣的脓疮。 你感觉教科书讲得不明不白,这不是你的智商问题,而是教材编写者的妥协问题。大多数非数学专业的微积分教材,甚至一部分名为数学分析的教材,在处理微分这个概念时,确实是在捣浆糊。他们试图在不引入线性代数、不引入流形、不引入对偶空间的前提下,强行解释一个本质上属于这些领域的概念。结果就是你看到的:语焉不详,逻辑断裂,只可意会不可言传。 先说结论:微分 d 确实是一个算子,dx 确实是一个基底,而 dy 是一个线性映射在特定向量上的作用结果。 但要讲清楚这一点,必须抛弃那种把微积分看作计算技巧集合的低级视角,进入现代数学的结构视角。 教科书之所以不敢这么写,是因为如果在讲大一微积分时就引入切空间和对偶空间的概念,99%的学生会当场挂科。于是,教材编选者们选择了一个偷懒的办法:用线性近似来糊弄过去。 咱们一层一层剥开来看。 第一层尴尬:导数都没讲利索,怎么讲微分 你在书上看到的微分定义,通常长这样:如果函数的增量可以写成 A 乘以 dx 加上一个无穷小量,那么 Adx 就是微分。这里面的 A 就是导数。 这种定义最大的问题在于它把导数和微分强行绑在了一起,而且是在一维实数的狭隘语境下绑定的。在一维情况下,导数是一个数,微分好像就是这个数乘以 dx。这让初学者产生了一个极其顽固的错觉:微分就是很小的增量,或者微分就是导数乘以一个标记。 大错特错。 在严谨的现代分析学中,特别是引入了泛函分析和微分几何的视角后,导数(Derivative)的本质不是一个数,甚至不是一个斜率。导数是一个线性映射(Linear Map)。 想象一下,我们有一个函数 f,它把一个空间映射到另一个空间。我们在某一点 x 附近观察这个函数。如果这个函数够平滑,那么在无限小的尺度下,它看起来就是平直的。这个平直的局部结构,就是切空间。 所谓的求导,实际上是在寻找一个最佳线性逼近。对于单变量函数,这个线性映射可以用一个数(斜率)来代表,这就是为什么大一新生觉得导数是个数。但是一旦到了多维空间,导数就必须是一个矩阵(雅可比矩阵)。 这里我们要引入一个关键概念:弗雷歇导数(Fréchet derivative)。 对于赋范线性空间之间的映射 f,如果存在一个连续线性算子 L,使得 f 在 x 点附近的增量可以被 L 作用在增量向量 h 上来逼近,且误差是关于 h 的高阶无穷小,那么这个线性算子 L 就是 f 在 x 点的导数。 注意,这里 L 是一个算子,是一个函数,而不是一个数。 那么微分是什么? 微分 df 就是这个线性算子本身。 或者是这个线性算子作用在某个特定的向量上。这里教科书就开始打架了。有的书把 df(x) 定义为那个线性算子 L,有的书把 dy 定义为 L(h)。 这就引出了你提到的 dx 是什么的问题。 第二层尴尬:dx 到底是什么鬼东西 这是最让学生崩溃的地方。有时候 dx 是一个无穷小量,有时候它是积分符号的一部分(仅仅是个括号),有时候它又是自变量的增量。 在严谨的数学体系(特别是流形上的微积分)中,dx 是一个线性泛函,是切空间对偶空间(余切空间)的一组基底。 咱们说人话。 假设我们在一个流形(比如弯曲的曲面)上,每一点都有一个切平面。切平面上的向量是切向量。所有的切向量构成了切空间。 现在,我们需要测量这些切向量。我们需要一个函数,吃进去一个向量,吐出一个数。这种吃向量吐数的线性函数,叫做1-形式(1-form)或者余切向量。 dx 就是这样一个吃向量的机器。 具体来说,在坐标系 x 下,dx 是一个把向量 v 投影到 x 轴方向上的函数。如果你给我一个向量 v = (3, 4),那么 dx(v) = 3,dy(v) = 4。 所以,当我们写下 dy = f'(x)dx 时,这不仅仅是一个代数等式,这是一个算子之间的等式。 等式左边 dy 是一个 1-形式。 等式右边 f'(x) 是一个系数(标量函数),乘以 dx 这个 1-形式。 这意味着,无论你喂给这两个东西什么样的切向量 v,它们吐出来的结果都是一样的。 dy(v) = f'(x) * dx(v)。 这就是为什么我们可以说 dy 是 dx 的线性组合。在高维情况下,这就变成了全微分公式: df = (?f/?x1)dx1 + (?f/?x2)dx2 + ... 这里的 d 是一个外微分算子(Exterior Derivative)。它把一个 0-形式(也就是标量函数 f)变成了一个 1-形式(df)。 你看,这才是严谨的定义。 d 是算子:把函数变成形式。 f 是 0-形式。 df 是 1-形式。 dx 是基底形式。 ?f/?x 是分量系数。 这个体系极其优美,逻辑闭环,没有任何含糊不清的地方。但是,这一套东西通常要到数学系大三学习《微分流形》或者《张量分析》的时候才会全盘托出。 对于大一工科生,或者普通数学分析教材,编书的人认为讲什么是对偶空间、什么是张量积简直是天方夜谭。所以他们选择了沉默,或者用“自变量的微分定义为自变量的增量”这种循环论证般的废话来搪塞。 这就导致了你说的:d 的定义不明不白,dx 仿佛是个幽灵。 第三层尴尬:高阶微分的巨坑 你提到了高阶微分 d?y。这是教科书最不负责任的地方。 大多数教材会告诉你,二阶微分 d2y 就是 f''(x)(dx)2。 然后告诉你,这玩意儿形式上是不变的,这叫一阶微分形式不变性。 但是,他们往往不告诉你,高阶微分没有形式不变性! 这是一个巨大的坑。 如果 x 是自变量,那么 d2y = f''(x)(dx)2 是成立的。 但是,如果 x 不是自变量,而是另一个变量 t 的函数 x(t),那么事情就变了。 根据链式法则,你会发现 d2y 会多出一项来。 因为 dx 现在也是变量了,d(dx) 不再是 0。 教科书在这里的处理往往是含糊其辞,告诉你“通常我们在自变量下讨论”。这直接导致学生在处理复杂变量代换,或者进入变分法、微分几何领域时,概念完全崩塌。 在现代观点下,高阶微分甚至不是一个定义良好的概念,除非你引入射流丛(Jet Bundle)或者把二阶导数看作是切丛上的映射。 在流形上,我们通常只谈论外微分。d 作用在 f 上得 df,d 作用在 df 上得 d2f。 但是,外微分有一个性质:d2 = 0。 这意味着在微分形式的意义下,二阶微分恒为零。 你看,这和微积分里的 d2y 完全是两码事。微积分里的二阶微分,实际上是在谈论二阶切丛上的二次型,或者是泰勒展开的二次项。而外微分谈论的是上同调。 这两套符号系统的冲突,教材从来不讲。学生只能靠自己悟。 为什么会出现这种情况? 这是一个历史遗留问题。 微积分的符号系统主要继承自莱布尼茨。莱布尼茨当年搞这套东西的时候,根本没有极限、实数理论、拓扑空间这些概念。他的脑子里就是无穷小量。dx 就是一个无限小的一段 x,dy 就是无限小的一段 y。 这套直观的理解非常极其好用。好用到物理学家和工程师根本离不开它。 你随便找个物理系教授,问他什么是微分。他会告诉你:把一个东西切成无限多份,每一份就是 d 什么什么。 但是数学家后来发现无穷小量会导致悖论(贝克莱主教的批评),于是柯西和维尔斯特拉斯搞出了 ??δ??δ 语言,用极限重构了微积分。 问题来了:地基换了(从无穷小量换成了极限),但是房子没拆(符号还是 dy, dx, ∫)。 这就导致了符号和定义的脱节。 我们在用极限的逻辑定义导数,却在用无穷小量的符号书写公式。 教科书为了照顾这种分裂,只能两头堵。一边告诉你 dx 不是无穷小,是增量;一边在积分换元的时候像操作分数一样操作 dx/du。 这种精神分裂,直到 20 世纪 60 年代鲁宾逊创立非标准分析,把无穷小量在一个超实数域上严格化了,才算给莱布尼茨平了反。或者,走刚才说的微分几何路线,把 dx 定义为形式。 但在基础教学中,我们依然卡在这个尴尬的中间状态。 实际场景佐证:热力学的混乱 咱们来看一个具体的场景,这绝对能让你感同身受。 学过热力学吗? 热力学第一定律:dU = TdS - pdV。 对于一个数学系出身、只学过严谨分析但没学过流形的人来说,这个公式简直是天书。 U 是函数,这没问题。 d 是微分算子,也没问题。 但是 T, S, p, V 是什么? 在物理学家眼里,这都是状态量。 在数学家眼里,这其实是流形上的微分形式的关系。 物理学家会很自然地写出: (?U/?S)_V = T 这是怎么来的?这是把 pdV 看作 0,两边除以 dS 得到的。 这种操作在数学分析教材里是被明令禁止的——“微分不能像分数一样随便除!” 但物理学家除得飞起,而且结果是正确的。 这说明什么?说明莱布尼茨的那套符号系统,隐含了余切空间的对偶性质,虽然物理学家可能没学过对偶空间,但他们直觉上用对了。 如果教科书能大大方方地承认:dy 和 dx 就是余切空间的向量,它们构成了局部坐标系下的基底,所以它们当然可以像代数符号一样运算(在张量代数的规则下)。 那学生就不会这么纠结了。 可惜,教科书为了避嫌,为了避免引入张量积,选择了把 dx 解释为“自变量增量”,这就彻底堵死了理解 dU = TdS - pdV 这种公式本质的道路。 如何建立严谨的体系? 如果你是一个对数学有追求的人,想跳出这个不明不白的泥潭,我建议你按以下路径重塑你的认知体系: 第一阶段:抛弃“数”的执念,拥抱“映射”。 要把函数 f 看作空间到空间的映射。 要把导数 Df 看作点 x 处的最佳线性逼近算子(矩阵)。 微分 df(x) 就是这个线性算子 Df(x)。 当它作用在向量 h 上时,df(x)(h) 才是具体的数值增量近似。 第二阶段:理解对偶空间。 线性空间 V 的对偶空间 V* 是所有线性泛函的集合。 如果 x1, ..., x? 是 V 的坐标函数,那么 dx1, ..., dx? 实际上构成了 V* 的一组基。 任何 1-形式(比如 df)都可以写成这组基的线性组合。 这就是 df = Σ (?f/?x?) dx? 的真谛。这是一个向量空间的基底展开式,而不是什么“微商乘以增量”。 第三阶段:理解外代数。 微分不仅仅是线性化,它还涉及到方向。 为什么二重积分换元会有雅可比行列式?那是楔积(Wedge Product)dx ∧ dy 的几何性质决定的。 dx ∧ dy 是一个反对称的张量,它度量的是有向面积。 这时候你再看 d2 = 0,就会明白它是外微分算子的拓扑性质,跟泰勒展开没半毛钱关系。 如果你现在正在被国内那些语焉不详的教材折磨,我有几条具体的建议: 1. 不要死磕定义,看定理。 国内教材在定义上往往畏手畏脚,但在定理叙述上通常还是严谨的。通过观察微分中值定理、泰勒公式、隐函数定理的描述,反向推导它在这个体系里到底把微分当什么。 2. 参考高观点的书。 去读卓里奇的《数学分析》。这是前苏联的传世经典,它在讲微积分的时候,非常自然地引入了现代观点,虽然难,但逻辑是通的。 或者读斯皮瓦克(Michael Spivak)的《流形上的微积分》(Calculus on Manifolds)。这本书很薄,但它用几十页的篇幅,把从欧氏空间到微分形式的逻辑讲得清清楚楚。它会告诉你,dx 就是一个投影函数,仅此而已。 3. 接受历史的混乱。 你要明白,我们在用 17 世纪的符号,讲 19 世纪的逻辑,以此为基础去理解 20 世纪的几何。这种错位感是必然存在的。 当你看到 dy = y'dx 时,心里要清楚: 在计算时,把它当数处理(莱布尼茨的遗产)。 在理解时,把它当线性形式处理(现代几何的观点)。 在证明时,把它当极限处理(分析学的根基)。 最后的碎碎念 数学教育是一个不断妥协的过程。如果在大一就把外代数和切丛拍在学生脸上,数学系可能就没人了。 但是,这种妥协不应该变成欺骗。 优秀的教材应该在简单的表述背后,预留出通往严谨定义的接口,而不是用“无穷小量”这种含糊的概念把路堵死。 你感到痛苦,是因为你试图用逻辑去弥合教材编写者的教学法妥协。 这种痛苦是你进阶的阶梯。 当你有一天能笑看 dy 既是无穷小又是线性泛函时,你就真正懂了。 d 是算子,dx 是基底,微积分是关于变化的线性代数。 这一句话,顶一万句“自变量的增量”。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
因为几乎所有的工科微积分教材(同济版为代表)在讲微分的时候,都在试图掩盖一个事实:导数和微分,根本就是两码事,但在低维空间里它们恰好长得一样。 这就好比在二维平面上,复数和向量都能用 (x, y) 表示,你就误以为它俩是一回事。 教科书最大的误导在于,它太想让你把微分理解成 一个很小的数。 你想想,牛顿和莱布尼茨当年搞微积分的时候,确实是把 dx 当作一个 无穷小 的量。这就好比早期的汇编语言,直接操作内存地址。这种理解非常直观,物理学家特别喜欢。你把它切成无数小块,每一块就是 dx。 但是这玩意儿在数学上是不严谨的。如果你承认有 无穷小 这种实数存在,那 1 除以无穷小是啥?第一次数学危机就是这么来的。 后来柯西他们搞出了 \epsilon-\delta 语言,把大厦地基重修了一遍。按理说,这时候 dx 作为 无穷小量 的概念就该被废除了。但是!莱布尼茨发明的那套符号系统 dy/dx 实在是太好用了,好用到哪怕逻辑不对,大家也舍不得扔。 于是教材就开始 骑墙 了。 它先用极限严格定义了导数 f'(x)。这一步是严谨的。 然后它定义微分 dy = f'(x)\Delta x。注意,这里突然把 \Delta x 换成了 dx,告诉你对于自变量,dx = \Delta x。 这其实是一种 强行定义。 这就好比我在写代码,先定义了一个严谨的类 Class A,然后为了兼容旧代码,我硬生生写了个宏定义 #define B A,然后告诉你 B 就是 A。 教材这么做是为了让你在做积分的时候,能顺理成章地写出 \int f(x) dx,并且在使用换元法的时候,能像操作分数一样操作 dy 和 dx。 比如 y = y(u), u = u(x),那么 \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}。 如果不把 dy 和 dx 看作是可以独立运算的量,这个链式法则的记忆成本会高很多。 所以,教材的策略是:为了让你 算得爽,逻辑上就 糊弄 一下。对于99%的工科生来说,这够用了。因为他们以后只需要算算梁的弯曲,或者电路的响应,不需要去深究流形上的切丛。 但是对于你这种在这个问题上卡住的人,说明你的数学直觉非常敏锐。你察觉到了这个系统里的 Bug。 这里我必须要推荐一本神书,《卓里奇数学分析》。它是俄罗斯教材的巅峰。相比于国内教材的语焉不详,卓里奇从一开始就把 现代数学 的观点引入进来。或者是找一些专门针对国外数学体系的经典教材来互相对照,很多国外教材,特别是分析学这些,他们都不会把你当傻子,而是明明白白告诉你微分是线性映射。 76本国外经典教材,全方位覆盖代数、几何、分析、概率等核心领域 咱们把视角拉回到现代,拉回到数据科学和算法。 在机器学习里,我们天天搞梯度下降,搞反向传播。你见过哪个算法工程师在代码里写 无穷小量 吗?没有。 在现代数学和计算机科学里,微分的本质是 线性逼近。 你把函数 f 想象成一个复杂的非线性变换。比如一个深层的神经网络,或者一个复杂的曲面。 我们在某一点 x_0 附近,想要研究这个函数。非线性太难了,咱们搞不定。怎么办? 我们试图用一个 线性函数(直线、平面、超平面) 来模仿它。 微分,就是这个最佳的线性模拟器。 用公式说人话: f(x_0 + h) - f(x_0) = L(h) + o(h) 这里 h 是一个小位移(向量)。 L 是一个线性变换(Linear Map)。 o(h) 是高阶无穷小,也就是误差。 这个线性变换 L,就是函数在 x_0 处的微分,记作 df_{x_0}。 请注意,这里 df 不是一个数,它是一个 函数,一个 线性算子。它吃进去一个向量 h,吐出来一个数值,告诉你函数值大概变了多少。 这才是 d 的真面目:它是把非线性函数局部线性化的那个 算子。 回到你问的 d 是什么。 d 是一个 算子(Operator),它作用在函数 f 上,生成了一个新的东西 df(微分形式)。 而 dx 是什么?在现代观点下,x 也是一个函数(坐标函数),dx 就是坐标函数的微分。 这就解释了为什么 dy = f'(x)dx。 这不是除法,这是两个 线性映射 的相等关系。 左边是 dy(关于 y 的线性逼近),右边是 f'(x)(一个系数,或者矩阵)乘以 dx(关于 x 的线性逼近)。 它们作用在同一个向量 h 上时,结果是一样的。 如果你搞懂了这一点,你对微积分的理解就超过了90%的大学生。 这里插一个资源推荐。如果你想从 线性代数 的角度彻底搞懂微积分(这其实是正道),一定要看 3Blue1Brown 的视频。他的几何直觉是顶级的,特别是他讲 【合集】线性代数的本质 中英双语,能让你明白矩阵不仅仅是数字的方阵,而是空间的变换。看完这个,你再配合 Gilbert Strang 的公开课,或者参考 3Blue1Brown线性代数笔记 中英合集 来复盘,你会发现微积分里的雅可比矩阵瞬间就亲切了。 接下来咱们讲点你在普通教材里死活找不到答案的部分。 你问 dx 是未知数还是文字? 在实数域的一元微积分里,教材把它糊弄成一个增量 \Delta x。 但在高维空间,在流形(Manifold)上,在咱们做深度学习优化的时候,dx 有一个非常高大上的名字:余切向量(Cotangent Vector),或者是 1-形式(1-form)。 别被名字吓跑。咱们用算法的逻辑拆解它。 假设你有一个向量空间 V(比如切空间,想象成切线方向)。 在这个空间里,有两个主要的角色: 向量(Vector):比如速度、位移。咱们记作 v。对偶向量(Dual Vector):这是一个函数,它吃进一个向量,吐出一个数。这叫 线性泛函。 dx 就是一个对偶向量。 它的作用是啥?它的作用是 测量。 dx 是一个尺子,它量的是向量在 x 轴上的投影长度。 dy 是另一个尺子,它量的是向量在 y 轴上的投影长度。 所以,df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy 这个公式的意思是: 我们要计算函数 f 的变化量(df),怎么算? 我们把变化量分解成两部分: 第一部分是 x 方向的变化率(偏导数)乘以 x 方向的投影长(dx)。 第二部分是 y 方向的变化率乘以 y 方向的投影长(dy)。 这是一个内积! 或者说是梯度向量和位移向量的点积。 教材不明不白的地方在于,它不告诉你 dx 是基底。 在对偶空间里,\{dx, dy\} 是一组 基底(Basis)。任意一个微分 df 都是这组基底的线性组合。 这就像我们在图像处理里,把一张图分解成 RGB 三个通道。dx 就是 R 通道,dy 就是 G 通道。导数 \frac{\partial f}{\partial x} 就是 R 通道的像素值(系数)。 这套理论在 张量分析 和 微分几何 里是基石。但在大一高数里,老师不敢讲,怕学生当场退学。于是就变成了“它是一个很小的数”。 如果你对这个视角感兴趣,想看看真正的数学大厦长什么样,推荐你去翻翻 Loring Tu的《An Introduction to Manifolds》 的前几章。不用全看,看懂切空间和微分形式那部分就行。你会发现,原来 d 是一个 外微分算子,满足 d^2 = 0。这个性质 d^2=0 甚至直接关联到拓扑学里的 德拉姆上同调。看,这才是严谨体系的味道。 你问到了高阶微分 d^n y。这绝对是普通教材最 坑爹 的地方。 很多教材会给你推导:d^2 y = f''(x) (dx)^2。 然后告诉你,这玩意儿形式不变性只在 x 是自变量时成立。如果 x 是中间变量,这公式就不成立了。 这叫什么严谨体系?这叫打补丁! 一个数学定义,居然还依赖于变量是“自变量”还是“中间变量”这种物理身份?简直是离谱。 事实是:在现代微分几何中,通常根本不定义高阶微分 d^2 f 这种东西。 因为 df 是一个 1-形式(1-form)。对 1-form 再求外微分 d(df),根据外微分的性质,结果恒等于 0。 所以在流形上,没有二阶微分这个概念。 我们在优化算法里用的 二阶导数(海森矩阵 Hessian Matrix),它不是一个微分形式,它是一个 双线性形式。 教材为了强行把 f''(x) 写成 d^2y / dx^2 的形式,搞出了一套非常不自然的定义。这纯粹是为了凑那个莱布尼茨的记号。 我的建议是:忘掉高阶微分。 在实际工作中,无论是做金融风控模型,还是做自动驾驶的轨迹规划,我们只用 泰勒展开。 f(x+h) \approx f(x) + f'(x)h + \frac{1}{2} h^T H h 这里 H 是海森矩阵。这就够了。 别去纠结 d^2 y 到底是个什么对象,它在现代数学框架里是一个 畸形儿。 那么为什么很多教科书都讲不清楚?因为这里面有一个巨大的 认知断层。 在这个断层的一边,是 古典分析(17-19世纪)。代表人物是牛顿、莱布尼茨、欧拉。他们的直觉极强,物理意义明确,但是逻辑上有漏洞。目前的工科微积分(Calculus)主要教这个。因为好用,能算题,能造桥。 在断层的另一边,是 现代分析(20世纪以后)。代表是流形、泛函、拓扑。这里面逻辑严丝合缝,但抽象程度极高。这里讲的是 Analysis(数学分析)甚至 Manifolds。 大多数教科书试图用古典的语言去解释现代的逻辑,或者用现代的逻辑去圆古典的符号。 结果就是两头不讨好。讲严谨了,工科生听不懂;讲直觉了,理科生觉得你在扯淡。 六、 给你的一点过来人的建议 既然你问了这个问题,说明你不是一个满足于 当调包侠 的人。你想搞懂底层的 源码。这非常好。 在IT行业,尤其是搞算法这块,这种 Deep Dive 的能力是核心竞争力。别人只会调 sklearn.linear_model,你知道梯度下降背后的几何意义,你知道海森矩阵怎么影响收敛速度,你知道正则化其实是引入了先验分布。这就是区别。 针对你的困惑,我有几条非常具体的建议,不玩虚的: 把微分看作 线性逼近,而不是无穷小。 以后看到 dy,脑子里直接翻译成:切线(或者切平面)上的增量。 看到 dx,翻译成:一个把向量映射为它第一个坐标分量的线性函数。看一看现代视角的实战应用:自动微分(Automatic Differentiation)。 你在用 PyTorch 或 TensorFlow 的时候,写了一行 loss.backward()。 机器是怎么算出梯度的? 它不是在做 lim?Δx→0limΔx→0?,那是数值微分,误差大且慢。 它做的是 计算图(Computational Graph) 的 链式法则 传播。 在这里,每一个节点都是一个运算,每一条边传递的都是 雅可比矩阵(或者向量-雅可比积)。 如果你想从代码层面彻底搞懂这个动态过程,建议去读一读 《动手学深度学习》(Dive into Deep Learning),这就是圈内大名鼎鼎的 d2l。李沐老师他们搞的,真的是保姆级教程,有理论有代码。或者如果你想更深入地看 PyTorch 是如何实现这些数学概念的,可以看看 动手学PyTorch建模与应用,你会发现那些抽象的数学符号在代码里变得无比具体。建立计算机科学的底层大局观。 你现在的困惑,本质上是对“黑盒”的不满足。要真正理解这些数学工具如何在计算机上跑起来,你需要补充一些硬核的计算机基础。我非常推荐你花时间看看这份 全网累计下载100w+次,瞬间让你起飞的计算机基础知识,把数据结构、算法和底层原理串起来。当你理解了计算机是如何存储浮点数、如何进行数值计算的,你对无穷小和误差的理解会上升一个维度。别死磕某些国内教材的定义。 有些教材的定义是为了 考试 服务的。如果你发现逻辑不通,多半是书写得烂。直接去查维基百科的英文词条,或者翻阅 GTM (Graduate Texts in Mathematics) 系列里的基础书。比如 Rudin 的《Principles of Mathematical Analysis》(著名的蓝皮书),虽然难,但是它绝对不会骗你。它不会跟你说无穷小,它会跟你说拓扑、测度。实际案例佐证:自动微分(Automatic Differentiation)。 你在用 PyTorch 或 TensorFlow 的时候,写了一行 loss.backward()。 机器是怎么算出梯度的? 它不是在做 \lim_{\Delta x \to 0},那是数值微分,误差大且慢。 它做的是 计算图(Computational Graph) 的 链式法则 传播。 在这里,每一个节点都是一个运算,每一条边传递的都是 雅可比矩阵(或者向量-雅可比积)。 这就是微分的现代应用:组合函数的线性化传递。 你要是理解了这一点,你就理解了为什么深度学习能 work。因为它本质上就是把一个巨大的复杂函数,分解成无数个简单的函数(加减乘除、ReLU),然后利用 微分(线性逼近) 的链式法则,把误差传回来。 教科书不明不白,是因为它们背负了太沉重的历史包袱,试图在给非数学专业的学生科普时,牺牲了逻辑的严密性。 这不是你的错。 对于我们这些在行业里摸爬滚打的人来说,d 就是 Linearization(线性化),dx 就是 Basis of Dual Space(对偶基底)。 建立起 线性代数 的视角,抛弃 无穷小 的执念。你会发现,数学其实比教科书上写的要干净漂亮得多。 在这个信息爆炸的时代,能沉下心来问这种 原理 性问题的人不多了。保持这份好奇心和钻牛角尖的劲头。当年我死磕这些概念的时候,觉得百无一用,后来做复杂系统建模和高维优化算法的时候,这些直觉救了我的命。有些东西,只有当你理解了最底层的逻辑,才能在上面建起万丈高楼。 送礼物 还没有人送礼物,鼓励一下作者吧 |
|
|
| [收藏本文] 【下载本文】 |
| 工程技术知识 最新文章 |
| 缺乏地理常识,是种怎样的体验? |
| 如何评价大熊猫的颜值? |
| 明明人类统治地球都几百万年了,为什么百兽 |
| 在我国开始大规模建设高铁之前的讨论中,「 |
| 为什么现在央视不报道二氧化碳合成淀粉了? |
| 为什么大家都不提中国空间站了? |
| 世界最“伟大”的水果是什么? |
| 如果全球都降到零下50-100度,在提前一个月 |
| 有没有动物一直近亲繁殖而没有灭绝的? |
| 高铁的作用被高估了吗? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |