| |
|
| 知识库 -> 工程技术知识 -> 在数学的学习过程中,你见过最妙的数学证明是什么? -> 正文阅读 |
|
|
[工程技术知识]在数学的学习过程中,你见过最妙的数学证明是什么? |
| [收藏本文] 【下载本文】 |
|
在中学和大学以及研究生阶段的数学学习中,我们总能见到许许多多的数学证明,它们中有一些证明的思路一定是相当精彩的,但也许是受到学识的有限,在证明的初次遇… |
|
中学时期曾在Matrix67的博客里看到过一个巧妙的题目,原题来自2014 年印度全国奥林匹克数学竞赛。 求证:对于任意正整数 n" role="presentation">nn 而言, [n]+∑i=1n[ni]" role="presentation">[n]+∑i=1n[ni]\left[ \sqrt{n}\right]+\sum_{i=1}^{n}{\left[ \frac{n}{i} \right]} 总是偶数, [x]" role="presentation">[x][x] 表示不超过 x" role="presentation">xx 的最大整数。 这题的常规解法难度并不大,使用数学归纳法外加一点点点注意力就好: 令 f(x)=[x]+[x1]+[x2]+[x3]+...+[xx]" role="presentation">f(x)=[x]+[x1]+[x2]+[x3]+...+[xx]f(x)=\left[ \sqrt{x} \right]+\left[ \frac{x}{1} \right]+[\frac{x}{2}]+[\frac{x}{3}]+...+[\frac{x}{x}] 显然 f(1)=2" role="presentation">f(1)=2f(1)=2 ,成立。假设 f(k)" role="presentation">f(k)f(k) 是个偶数,我们来证明 f(k+1)" role="presentation">f(k+1)f(k+1) 也是偶数。 注意到 [k+1i]−[ki]=1" role="presentation">[k+1i]?[ki]=1[\frac{k+1}{i}]-[\frac{k}{i}]=1 ,当且仅当 k+1" role="presentation">k+1k+1 能被 i" role="presentation">ii 整除;否则它将等于0。 我们记 σ(k)" role="presentation">σ(k)\sigma(k) 为 k" role="presentation">kk 的因数个数,于是有 f(k+1)−f(k)=σ(k+1)+[k+1]−[k]" role="presentation">f(k+1)?f(k)=σ(k+1)+[k+1]?[k]f(k+1)-f(k)=\sigma(k+1)+[\sqrt{k+1}]-[\sqrt{k}] 注意正整数的因数个数总是偶数(因数都是成对的嘛),除非它恰好是一个完全平方数。 于是 σ(k+1)" role="presentation">σ(k+1)\sigma(k+1) 是个偶数,除非 k+1" role="presentation">k+1k+1 是个完全平方数。 而当 k+1" role="presentation">k+1k+1 是完全平方数时, [k+1]−[k]=1" role="presentation">[k+1]?[k]=1[\sqrt{k+1}]-[\sqrt{k}]=1 ,否则它将等于0。 于是 f(k+1)−f(k)" role="presentation">f(k+1)?f(k)f(k+1)-f(k) 总是个偶数,再由假设,我们得到原命题成立。 这个证明很稳健,但是不够优雅,一位名叫David Angell的网友给了一个很优雅的证明: 注意到—— [n1]+[n2]+[n3]+...+[nn]" role="presentation">[n1]+[n2]+[n3]+...+[nn]\left[ \frac{n}{1} \right]+[\frac{n}{2}]+[\frac{n}{3}]+...+[\frac{n}{n}] 这个东西,恰好是第一象限中位于曲线 y=nx" role="presentation">y=nxy=\frac{n}{x} 下方(含接触)的整数格点数目诶!(*^▽^*) 我们把这样的格点分为两类:A类是位于直线 y=x" role="presentation">y=xy=x 之上的,B类是位于直线 y=x" role="presentation">y=xy=x 之外的。 显然B类点的数目是偶数,因为B类点都是关于直线 y=x" role="presentation">y=xy=x 对称分布的。 接下来讨论A类点,显然A类点的坐标都是 (a,a)" role="presentation">()(a,a)(a,a) ,其中 a2" role="presentation">a2a^{2} 不超过 n" role="presentation">nn ,所以A类点的数目恰好是 [n]" role="presentation">[n][\sqrt{n}] 。 那么原式的意义就是B类点的数目(偶数个)加上A类点的数目( [n]" role="presentation">[n][\sqrt{n}] 个),再额外加一个 [n]" role="presentation">[n][\sqrt{n}] ,这个结果显然是偶数。 证毕。 Matrix67.com - Home Matrix67的博客至今还在更新,感谢他让中学阶段的我得以一窥数学殿堂的窗棂间透出的光。 |
|
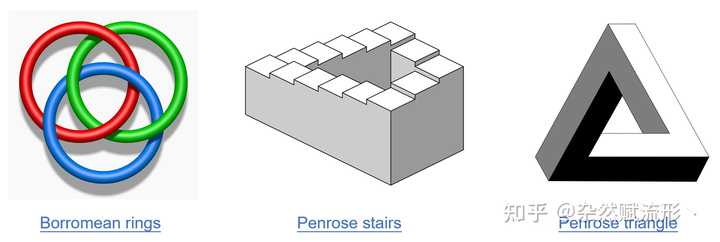
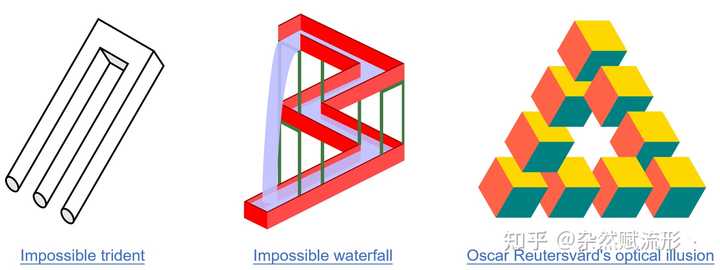
介绍一个高中生都能看懂的均值不等式的证明。 众所周知,对于正实数 a1,…,an∈R+" role="presentation">a1,…,an∈R+a_1,\dots,a_n\in \mathbb{R}^+ ,我们有以下 AM-GM 不等式成立: a1a2⋯ann≤a1+⋯+ann." role="presentation" style="font-size: 100%; display: inline-block; position: relative;">a1a2?ann≤a1+?+ann.\sqrt[n]{a_1a_2\cdots a_n} \leq \frac{a_1 + \cdots + a_n}{n}.\\关于它的证明方法也有很多,常见的是基于归纳的证明,也有不少非归纳证明方法。而分析学大师 Horst Alzer 在 1997 年就给出了一个极为精彩的证明方法[1]。 我们可以证明一个更强的不等式,对于任意正实数 a1,…,an" role="presentation">a1,…,ana_1,\dots, a_n 和 p1,…,pn" role="presentation">p1,…,pnp_1,\dots,p_n ,且 ∑i=1npi=1" role="presentation">∑i=1npi=1\sum_{i=1}^{n}p_i = 1 ,都有: a1p1a2p2⋯anpn≤p1a1+p2a2+⋯+pnan." role="presentation" style="font-size: 100%; display: inline-block; position: relative;">a1p1a2p2?anpn≤p1a1+p2a2+?+pnan.\color{crimson}{a_1^{p_1} a_2^{p_2}\cdots a_n^{p_n} \leq p_1 a_1 +p_2 a_2 +\cdots + p_n a_n.}\\记 G=a1p1a2p2⋯anpn" role="presentation">G=a1p1a2p2?anpnG=a_1^{p_1} a_2^{p_2}\cdots a_n^{p_n} , A=p1a1+p2a2+⋯+pnan" role="presentation">A=p1a1+p2a2+?+pnanA= p_1 a_1 +p_2 a_2 +\cdots + p_n a_n 。不失一般性,我们可以假设 a1≤⋯≤an" role="presentation">a1≤?≤ana_1\leq \cdots \leq a_n 。显然 a1≤G≤an" role="presentation">a1≤G≤ana_1\leq G\leq a_n ,所以必定存在某个 k" role="presentation">kk ,使得 ak≤G≤ak+1" role="presentation">ak≤G≤ak+1a_{k}\leq G\leq a_{k+1} 。从而有 ∑i=1kpi∫aiG(1t−1G)dt+∑i=k+1npi∫Gai(1G−1t)≥0," role="presentation" style="font-size: 100%; display: inline-block; position: relative;">∑i=1kpi∫aiG(1t?1G)dt+∑i=k+1npi∫Gai(1G?1t)≥0,\sum_{i=1}^{k} p_i \int_{a_i}^{G} \left(\frac{1}{t} - \frac{1}{G}\right) \mathrm{d}t + \sum_{i=k+1}^{n} p_i \int_{G}^{a_i} \left(\frac{1}{G} - \frac{1}{t}\right)\geq 0,\\这是因为括号里的表达式都是恒大于等于零的。上式可变形为: (∑i=k+1npi∫Gai1Gdt−∑i=1kpi∫aiG1Gdt)−(∑i=k+1npi∫Gai1tdt−∑i=1kpi∫aiG1tdt)=(∑i=k+1npi∫Gai1Gdt+∑i=1kpi∫Gai1Gdt)−(∑i=k+1npi∫Gai1tdt+∑i=1kpi∫Gai1tdt)=∑i=1npi∫Gai1Gdt−∑i=1npi∫Gai1tdt≥0" role="presentation">(∑i=k+1npi∫Gai1Gdt?∑i=1kpi∫aiG1Gdt)?(∑i=k+1npi∫Gai1tdt?∑i=1kpi∫aiG1tdt)=(∑i=k+1npi∫Gai1Gdt+∑i=1kpi∫Gai1Gdt)?(∑i=k+1npi∫Gai1tdt+∑i=1kpi∫Gai1tdt)=∑i=1npi∫Gai1Gdt?∑i=1npi∫Gai1tdt≥0\begin{align} &\left(\sum_{i=k+1}^n p_i \int _{G}^{a_i }\frac{1}{G}\, \mathrm{d}t - \sum_{i=1}^{k}p_i \int_{a_i}^{G} \frac{1}{G} \, \mathrm{d}t\right) -\left( \sum_{i=k+1}^n p_i \int_{G}^{a_i}\frac{1}{t}\,\mathrm{d}t - \sum_{i=1}^{k}p_i \int_{a_i}^{G} \frac{1}{t}\, \mathrm{d}t \right)\\[.2cm] ={}&\left(\sum_{i=k+1}^n p_i \int _{G}^{a_i }\frac{1}{G}\, \mathrm{d}t \color{red}{+} \sum_{i=1}^{k}p_i \int_{\color{red}{G}}^{\color{red}{a_i}} \frac{1}{G} \, \mathrm{d}t\right) -\left( \sum_{i=k+1}^n p_i \int_{G}^{a_i}\frac{1}{t}\,\mathrm{d}t \color{red}{+}\sum_{i=1}^{k}p_i \int_{\color{red}{G}}^{\color{red}{a_i}} \frac{1}{t}\, \mathrm{d}t \right)\\[.2cm] ={}&\sum_{i=1}^{n}p_i \int_{G}^{a_i} \frac{1}{G}\,\mathrm{d}t - \sum_{i=1}^{n} p_i \int_{G}^{a_i} \frac{1}{t}\,\mathrm{d}t \geq 0 \end{align} 将最后的积分计算出来: \begin{align} \sum_{i=1}^{n}p_i \int_{G}^{a_i} \frac{1}{G}\,\mathrm{d}t &=\sum_{i=1}^{n} p_i\frac{a_i - G}{G} = \frac{A}{G} -1,\\[.2cm] \sum_{i=1}^{n} p_i \int_{G}^{a_i} \frac{1}{t}\,\mathrm{d}t&=\sum_{i=1}^{n} p_i (\ln a_i - \ln G) = \ln \prod_{i=1}^{n} a_i^{p_i} - \ln G =0. \end{align}\\于是我们得到了 \dfrac{A}{G} - 1 \geq 0 ,这正是我们要证明的不等式 A\geq G 。而等号成立的条件则是我们最开始引入的积分结果为零,即被积函数均为零,也即 a_1 =\cdots =a_n = G 。 \Box 如果 p_1=\cdots = p_n = \dfrac{1}{n} ,上述不等式则又回到了我们熟悉的均值不等式。 另一个极其优雅的例子是:利用代数拓扑里的上同调群来证明不可能图形的「不可能性」。 不可能的图形是指在现实世界中不可能存在的物体,它们只可能存在于二维空间之中,利用人类视觉系统瞬间意识来对一个二维图形向三维投射,从而形成的光学错觉。 一些著名的例子如下图所示: |
|
|
|
|
|
或许你也联想到了《纪念碑谷》游戏里各种光怪陆离的建筑: |

|
|
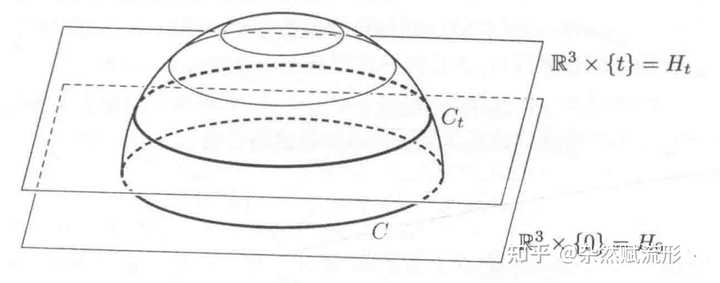
《纪念碑谷》里的游戏地图(中、右),很明显在致敬埃舍尔 1961 年的作品《瀑布》(左) 从直觉上来说,这些不可能图形的不可能性是相当「显然」的。但数学毕竟不是语文,又该如何严谨地证明它们的「不可能性」呢。 这部分内容我在另一个回答里详细论述了证明方法,在此便不重复了,感兴趣的可以移步以下回答: 例如:彭罗斯三角形我们处理的对象是上同调群 H^1(X,\mathbb{R}^+) 、彭罗斯阶梯我们处理的对象是上同调群 H^{1}(X,\mathbb{Z}_2) 。 另一方面,对于 Borromeo 链环的不可能性证明也非常有趣,即: Borromeo 链环不可能由三个刚性的正圆构成。 最早是 Freedman 和 Skora 在1987 年的一篇文章里给出的证明[2],尽管其中的几何直觉非常优雅,但解释起来却相对冗长,这部分内容的通俗解释可以参见《数学天书中的证明》第十五章[3]。 |
|
|
从圆形穹顶看「电影」 参考^ALZER, H. A NEW REFINEMENT OF THE ARITHMETIC MEAN-GEOMETRIC MEAN INEQUALITY. The Rocky Mountain Journal of Mathematics, 27(3), 663–667. (1997)^Michael H. Freedman, Richard Skora "Strange actions of groups on spheres," Journal of Differential Geometry, J. Differential Geom. 25(1), 75-98, (1987)^Martin Aigner. Günter M. Ziegler. Proofs from THE BOOK. 冯荣权. 宋春伟. 宗传明. 李璐. [译] |
|
题目:证明任意9个不同的实数 x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9, 总存在其中两个数 x_j">x_i>x_j 满足(1+\sqrt2)(x_i-x_j).\end{align*}">\begin{align*}x_ix_j+1>(1+\sqrt2)(x_i-x_j).\end{align*} ******************** | | | | | 证明见下方。 | | | | | ******************** 证明:令 x_k=\tan \theta_k,\theta_k\in (-\pi/2,\pi/2)。根据鸽巢原理总有 \theta_i,\ \theta_j 满足\begin{align*}\frac{1+x_ix_j}{x_i-x_j}=\frac{1+\tan\theta_i\tan\theta_j}{\tan\theta_i-\tan\theta_j}=\cot(\theta_i-\theta_j)>\cot\dfrac{\pi}{8}=1+\sqrt{2}.\end{align*} |
|
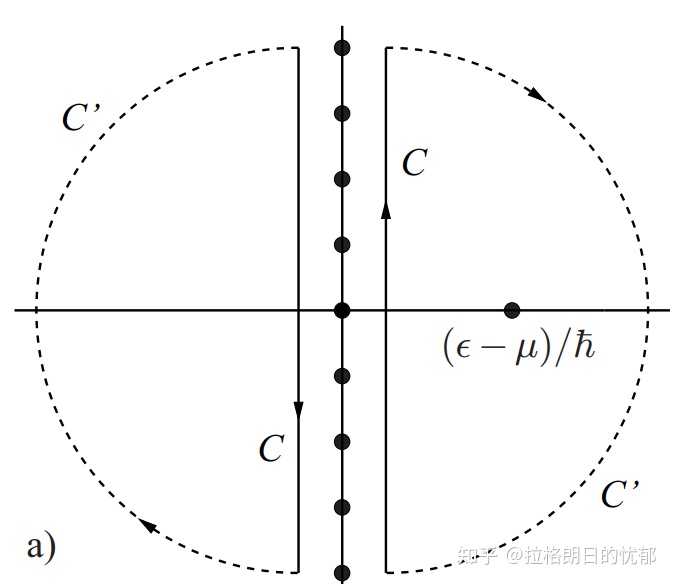
虚频求和换积分,尽管是凝聚态物理中最基础的技巧,但初见时惊为天人,现在依然经常感慨其结构的优雅。 \lim_{\eta\rightarrow 0+}\frac{1}{\beta}\sum_n\frac{e^{i\omega_n\eta}}{i\omega_n-(\epsilon_k-\mu)}=\pm\frac{1}{e^{\beta(\epsilon_k-\mu)}\pm 1} 这个式子证明也很简单,已知 1/(e^{\beta z}\pm 1) 在复平面上的pole是 z_n^F=i\pi(2n+1)/\beta 或者 z_n^B=i2n\pi /\beta 。利用留数定理,可以证明下面这个式子成立: \lim_{\eta\rightarrow 0^+}\frac{1}{2\pi i}\int_C dz \frac{e^{\eta z}}{z-(\epsilon_k-\mu)}\frac{\mp 1}{e^{\beta z}\pm 1}=\lim_{\eta\rightarrow 0+}\frac{1}{\beta}\sum_n\frac{e^{i\omega_n\eta}}{i\omega_n-(\epsilon_k-\mu)} |
|
|
图来自Stoof的Ultracold Quantum Fields中的7.2图 这里的回路 C 是绕着虚轴的,然后只需要证明上面式子的左边等于费米/玻色分布就可以了。 接着只需要在回路 C 的外边接一个无穷大但是不包括虚轴的回路 C' ,两个回路加起来就是绕着无穷远做一个回路积分,很明显能看出来 \frac{e^{\eta z}}{z-(\epsilon_k-\mu)}\frac{\mp 1}{e^{\beta z}\pm 1} 这玩意儿在无穷远处贡献是0,所以俩回路积分加起来等于0。而绕着 C' 的回路积分只有一个pole,就是 z=\epsilon_k-\mu ,再次对 C' 的积分用一次留数定理,马上就得到 \lim_{\eta\rightarrow 0^+}\frac{1}{2\pi i}\int_C dz \frac{e^{\eta z}}{z-(\epsilon_k-\mu)}\frac{\mp 1}{e^{\beta z}\pm 1}= \pm\frac{1}{e^{\beta(\epsilon_k-\mu)}\pm 1} 也就证完了。这种技巧在凝聚态场论里面属于最初级但是最实用的技巧,其巧妙地将求和转化为围道积分,进而用留数定理把求和解决掉,最终得到了一个费米/玻色分布的形式。 |
|
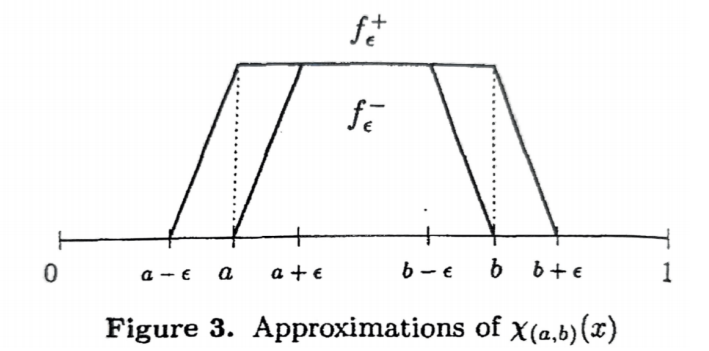
再看一次还是很感动: Weyl等分布定理。在证明中,它把对点的计数问题转化成了对特征函数的求和问题,将数论和微积分两个不同的板块联系在了一起。 Question: 设 q=\frac{b}{a}\in \mathbb{Q} 是有理数, nq 的小数部分具有怎样的分布?如果 \gamma\in \mathbb{R}\backslash\mathbb{Q} 是无理数, n\gamma 的小数部分具有怎样的分布? 当 q=\frac{b}{a} ( a,b 既约)是有理数时,容易证明 \exists x, y\in \mathbb{Z},s.t. ax+by=1 ,从而 :~n\in \mathbb{Z}\}=\{\frac{1}{a},\frac{2}{a},\dots,\frac{a-1}{a},0\}\tag{1}">\{<nq>:~n\in \mathbb{Z}\}=\{\frac{1}{a},\frac{2}{a},\dots,\frac{a-1}{a},0\}\tag{1} 是有限集。问题在于当 \gamma 是无理数时,集合 :~n\in\mathbb{Z}\}">\{<n\gamma>:~n\in\mathbb{Z}\} 将是一个无限集(若 =,"><i\gamma>=<j\gamma>, 则 i\gamma-j\gamma=n\in\mathbb{Z} ,这与 \gamma 是无理数矛盾)。这个集合在区间 [0,1) 上的分布是怎样的? Weyl 告诉我们它们是等分布的。 Definition:设 \xi_1,\xi_2,\dots,\xi_n,\dots 是一列定义在 [0,1) 上的序列,如果它们对于任意 (a,b)\subseteq[0,1) 非退化,满足: \lim_{N\to +\infty}\frac{1}{N}\#\{1\leq n\leq N:~\xi_n\in(a,b)\}=b-a\tag{2} 则称 \{\xi_n\}_{n=1}^{+\infty} 在区间 [0,1) 上等分布。 直观上看,只要我们取的 \xi_n 足够多,那么每一个子区间包含的 \xi_n 的比例是一样多的。而Weyl告诉我们: Theorem: 若 \gamma\in \mathbb{R}\backslash\mathbb{Q} 是无理数,则 \}_{n=1}^{+\infty}">\{<n\gamma>\}_{n=1}^{+\infty} 在 [0,1) 上等分布。 我们实际上要证明 \in (a,b)\}=b-a\tag*{}">\lim_{N\to +\infty}\frac{1}{N}\#\{1\leq n\leq N:~<n\gamma>\in (a,b)\}=b-a\tag*{} 对所有 (a,b) 成立,自然就涉及到对集合 \in (a,b)\}">\{1\leq n\leq N:~<n\gamma>\in (a,b)\} 大小的估算,问题是这要怎么做到呢?如何将在 (a,b) 里的选出来,不在 (a,b) 中的去除掉?没错,就是用特征函数。我们引入特征函数: \chi_{(a,b)}(x)=\begin{cases} 1 & x\in(a,b);\\ 0& x\notin (a,b).\end{cases}\tag{3} 并且将其作周期为 1 的延拓, 我们仍将作周期延拓后的函数记为 \chi_{(a,b)} 。此时, \chi_{(a,b)} 就成为了一个周期阶梯函数。我们将要证明的式子改写一下,就有,即证: \lim_{N\to +\infty}\frac{1}{N}\sum_{n=1}^{N}\chi_{(a,b)}(n\gamma)=\int_0^1\chi_{(a,b)}(x) dx.\tag{4} 这样我们就把一个计数问题转化为了一个分析问题。注意这里 \chi 是阶梯函数,如果我们对分析学的方法足够熟悉的话,我们立刻就能想到我们可以先将 \chi 替换为一个连续函数 f 证明这个式子,然后再用连续函数逼近阶梯函数即可。 Lemma:设 f(x) 是定义在实数轴上的周期为 1 连续函数,则 \lim_{N\to +\infty}\frac{1}{N}\sum_{n=1}^N f(n\gamma)=\int_0^1f(x)dx. \tag{5} 我们的证明分三步: Step 1: 若 f(x)=e^{2\pi in x}(n\in \mathbb{Z}\backslash\{0\}) , 则 f(x) 满足上式。 这里的证明很简单,只需要用等比数列的求和公式代入计算即可。 Step 2: 若 f(x), g(x) 满足上式,则 f(x)+g(x), cf(x) 也满足上式。 直接代入验证即可。 Step 3: Lemma的证明。 通过Step 1 和Step 2, 我们知道任意三角多项式都满足(5)式。而我们又知道连续函数可以被三角多项式逼近,从而接下来就是各种关于 \varepsilon 的放缩了:设 f(x) 是满足引理条件的函数, P_n(x) 是一三角多项式,且满足 N ,使得: \begin{align*} &\left|\lim_{N\to +\infty}\frac{1}{N}\sum_{n=1}^N f(n\gamma)-\int_0^1f(x)dx\right|\\ &=\frac{1}{N}\sum_{k=1}^N\left|f(k\gamma)-P_n(k\gamma) \right|+\left|\int_0^1 P_n(x)-f(x)dx\right|+\left|\frac{1}{N}\sum_{k=1}^N P_n(k\gamma)-\int_0^1 P_n(x)dx\right|\\ &<\varepsilon \end{align*}\tag{6} 从而我们完成了引理的证明。现在,我们考虑如下两个连续函数: |
|
|
就能完成Weyl等分布定理的证明了。 这个定理的证明似乎每一步都很轻松,但是却意外地将两个看似不相关地领域联系在了一起。第一次看完这个定理的证明非常震撼,现在即使再一次看到这个定理的证明也依旧觉得美妙~~ 上面讲的是分析学中的一个例子,下面讲一个代数学中的例子。我们在高等代数中就学过了Cayley-Hamilton定理。当时由于我所学的是用矩阵去证明的,但是这个证明,实话说,如果不是刻意去记的话,过个一年两年就忘了。但是学过模论后,我学到了一个新证明,我想在今后很长一段时间都不会忘记这个证明了吧。 我们注意到这样一件事: 设 M 是一个有限生成的 R- 模(这里我们总是假设 R 是交换含幺的),那么 Hom_R(M,M) 就可以定义模结构: (\varphi+\psi)(a)=\varphi(a)+\psi(a);~(c\varphi)(a)=c\varphi(a) \tag{7} 容易证明定义的这种加法满足交换律,从而构成加法的阿贝尔群,对数乘的几条性质也容易验算,从而这确实构成一个模。特别地,若 a\in R , 我们定义映射 a_L:\substack{M\to M\\ m\mapsto am} \tag{8} 我们发现对任意 a\in R, \varphi 和 a_L 可交换,(乘法定义为复合)现在我们有 Theorem: 设 M 是有限生成的 R- 模,由 n 个元素生成,且 \varphi\in Hom_R(M,M); 设 I 是 R 的理想,且 \varphi(M)\subset IM. 则我们有关系: \varphi^n+a_1\varphi^{n-1}+\dots+a_n=0\tag{9} 其中 a_i\in I^i,1\leq i\leq n (等式两边都被看作是 M 的自同态)。 Proof: 设 M=R\omega_1+R\omega_2+\dots+R\omega_n , 现在既然 \varphi(M)\subset IM ,以及 M 有限生成,我们就能得到一系列等式: \begin{cases} \varphi(\omega_1)=a_{11}\omega_1+a_{12}\omega_2+\dots+a_{1n}\omega_n\\ \varphi(\omega_2)=a_{21}\omega_1+a_{22}\omega_2+\dots +a_{2n}\omega_n\\ \dots\\ \varphi(\omega_n)=a_{n1}\omega_1+a_{n2}\omega_2+\dots+a_{nn}\omega_n. \end{cases}\tag{10} 移项后立刻有: \sum_{j=1}^n (\varphi\delta_{ij}-a_{ij})\omega_j=0~~\forall1\leq i\leq n.\tag{11} 其中 \delta_{ij} 表示Kronecker符号这样我们就得到了一个齐次线性方程组,其系数就是 Hom_R(M,M) 中的元素。我们将方程组的系数提取出来构成矩阵 A ,并记这个矩阵的行列式为 D ,就有 A\begin{bmatrix} \omega_1\\ \omega_2\\ \dots\\ \omega_n \end{bmatrix}=0\tag*{} 两边同时乘上伴随: A^*A\begin{bmatrix} \omega_1\\ \omega_2\\ \dots\\ \omega_n \end{bmatrix}=\begin{bmatrix} D& 0&\dots\\ 0& D& \dots\\ \dots\\ 0& 0& \dots D \end{bmatrix}\begin{bmatrix} \omega_1\\ \dots\\ \omega_n \end{bmatrix}=0\tag{12} 从而 D 作为一个算子,作用在任何 \omega_i 上都等于 0 , 而 \omega_i 又是 M 的生成元,从而 D\equiv 0 , 而 D 又是关于 \varphi 的首一多项式,这样我们就完成了定理的证明。 我们在学习Cayley-Hamilton定理的证明时,老师告诉我们直接把矩阵 A 带进 |\lambda I-A|中的 \lambda 是错误的做法,现在看来这实际有一定的道理。 当然如果到此为止的话就太没意思了。我们现在用模论再来证明一个高代中的经典结论。在此之前,我们先给出: Lemma (Nakayama): 设 M 是一个有限生成的 R- 模, I 是环 R 的一个理想。若 M=IM ,则存在 a\in R,s.t~aM=0, ~a\equiv 1(\bmod~I). Proof: 取 \varphi=1_M 并运用Cayley-Hamilton定理: 1+a_1+a_2+\dots +a_n=0.\tag*{} 现在我们来证明 Theorem: 设 M 是一个有限生成的 R- 模。若 f: M\to M 是 R- 线性映射,且 f 是满射,则 f 是单射,从而是 M 的自同构。 Proof: 现在我们将 M 看作是 R[x]- 模: g(x)\cdot m=g(f)(m),~~\forall g(x)\in R[x].\tag{13} 特别地, x\cdot m=f(m) ,又因为 f 是满射,从而 xM=M ,由 Nakayama 引理,存在 y\in R[x] 使得: (1+xy)M=0 . 设 u\in \ker f , 则 (1+xy)(u)=0 , 将括号打开立刻就有 u=0 . |
|
|
| [收藏本文] 【下载本文】 |
| 工程技术知识 最新文章 |
| 缺乏地理常识,是种怎样的体验? |
| 如何评价大熊猫的颜值? |
| 明明人类统治地球都几百万年了,为什么百兽 |
| 在我国开始大规模建设高铁之前的讨论中,「 |
| 为什么现在央视不报道二氧化碳合成淀粉了? |
| 为什么大家都不提中国空间站了? |
| 世界最“伟大”的水果是什么? |
| 如果全球都降到零下50-100度,在提前一个月 |
| 有没有动物一直近亲繁殖而没有灭绝的? |
| 高铁的作用被高估了吗? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
|
娱乐生活:
电影票房
娱乐圈
娱乐
弱智
火研
中华城市
印度
仙家
六爻
佛门
风水
古钱币交流专用
钓鱼
双色球
航空母舰
网球
乒乓球
中国女排
足球
nba
中超
跑步
象棋
体操
戒色
上海男科
80后
足球: 曼城 利物浦队 托特纳姆热刺 皇家马德里 尤文图斯 罗马 拉齐奥 米兰 里昂 巴黎圣日尔曼 曼联 |
| 网站联系: qq:121756557 email:121756557@qq.com 知识库 |